Wenn Sie das kartesische Koordinatensystem verwenden, dann können Sie Positionen beschreiben.
1. Das kartesische Koordinatensystem
Wörter 1
https://www.phyx.at/wp-content/uploads/2017/06/m116w1-a.mp3
das System, die Koordinaten (Zahlenangaben zur Festlegung eines Punktes), das Koordinatensystem (System von Linien und Einheiten), die Achse (die Gerade), der Punkt, die Fläche, führen, schreiben, beschreiben, rechts, oben, schneiden (sich kreuzen), zunehmen, die Richtung, die Null, der Wert, der Nullpunkt
Wir verwenden zwei Achsen, um Punkte auf einer Fläche zu beschreiben. Die x-Achse führt nach rechts, die y-Achse führt nach oben. Die beiden Achsen schneiden sich im Nullpunkt. Die Pfeile zeigen in Richtung zunehmender Werte.
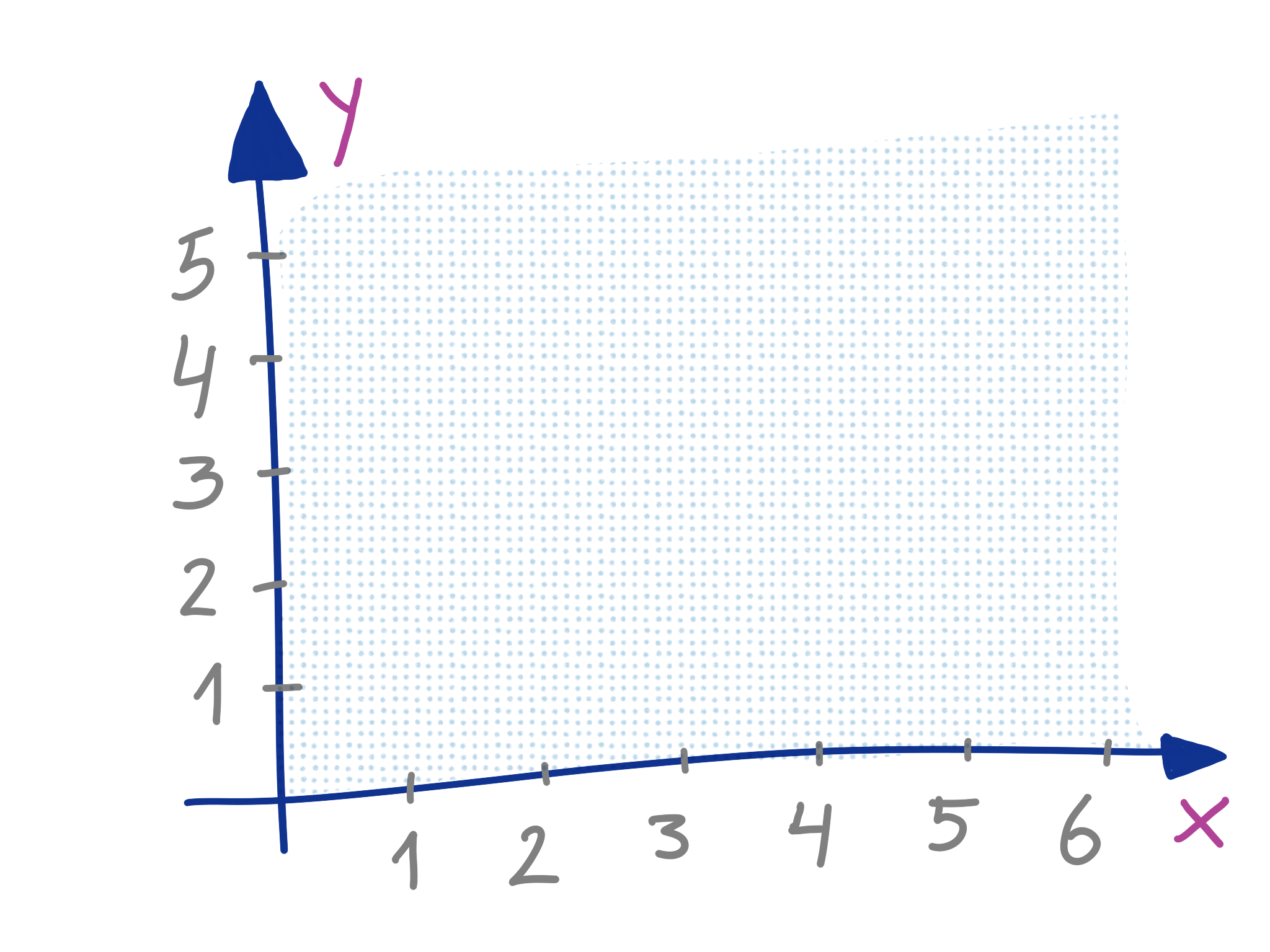
Jeder Punkt ist ein Stück von der x-Achse entfernt. Das ergibt seine y-Koordinate. Er ist auch ein Stück von der y-Achse entfernt. Das ergibt seine x-Koordinate. Wir nehmen immer die kürzesten Abstände.
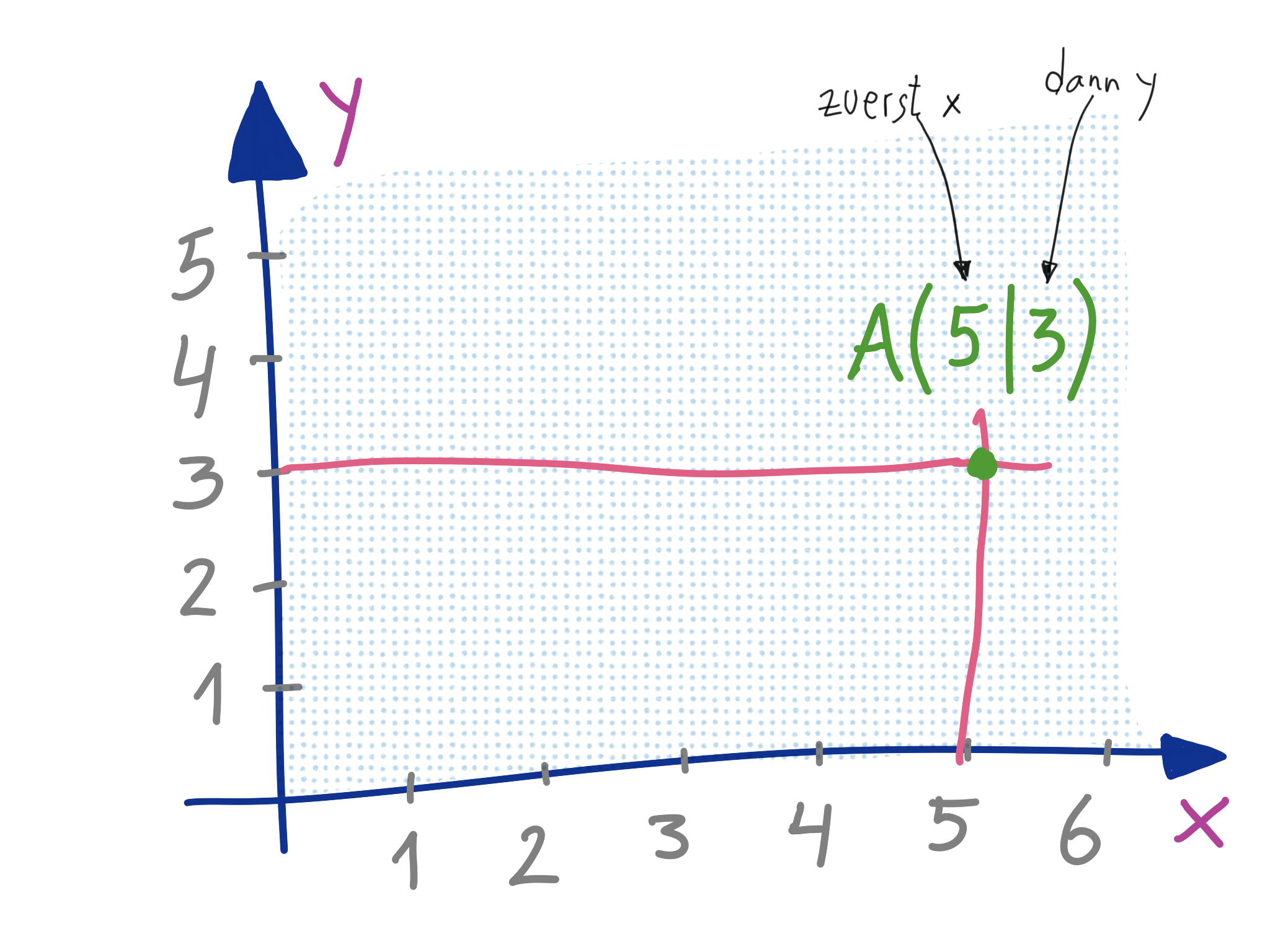
Es ist manchmal sinnvoll, auch negative Werte zu verwenden. Dann können wir das Koordinatensystem erweitern.
Übung
Welche Koordinaten haben die Punkte A, B, C und D?
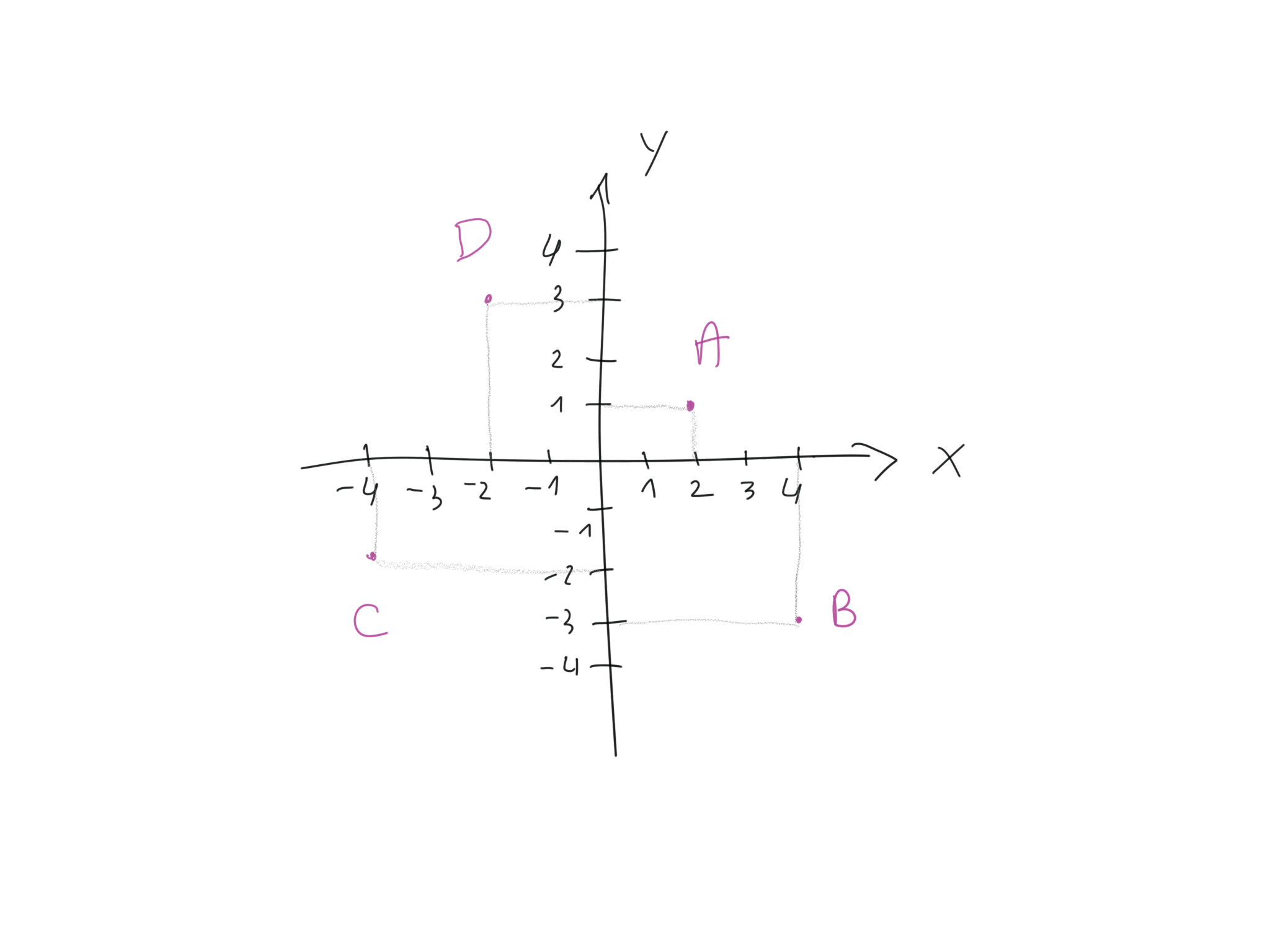
Lösung anzeigen
A (2|1), B (4|−3), C (−4|−2), D (−2|3)
Aufgabe
Koordinatensysteme können wir verwenden, wo immer wir Positionen von Objekten beschreiben möchten. Gerne auch bei Fenstern. Sie können auf die Bilder klicken, um sie zu vergrößern.
Wo wohnt Hubert Mair? Wo wohnt Mohamed Redha? Wo wohnt der Hausmeister?
Lösung anzeigen
Hubert Mair wohnt auf Position (2|3). Mohamed Redha wohnt auf Position (3|4). Der Hausmeister wohnt auf Position (6|2).
Wer wohnt auf Position (2|2)? Wer wohnt auf Position (7|1)? Wer wohnt auf Position (1|4)?
Lösung anzeigen
Auf Position (2|2) wohnt E. Hampl. Auf Position (7|1) wohnt Herr oder Frau Uhlig. Auf Position (1|4) wohnt Herr oder Frau Konstantinis.
Wo ist das grüne Windrad? Wo ist das rosa Windrad? Wo ist das blaue Windrad?
Lösung anzeigen
Das grüne Windrad ist bei Fenster (1|2), das rosa Windrad bei Fenster (2|2) und das blaue Windrad bei Fenster (3|2).
Welche Fenster sind offen?
Lösung anzeigen
Offene Fenster sind auf den Positionen (2|2) und (3|4).
Wo sind die Blumen? Wo sind die hölzernen Latten? Wo ist eine Jalousie zu 2/3 geschlossen?
Lösung anzeigen
Die Blumen sind auf Position (2|3), die hölzernen Latten auf den Positionen (1|2) und (2|2), und eine Jalousie ist auf Position (1|2) zu 2/3 geschlossen.
2. Weitere Koordinatensysteme
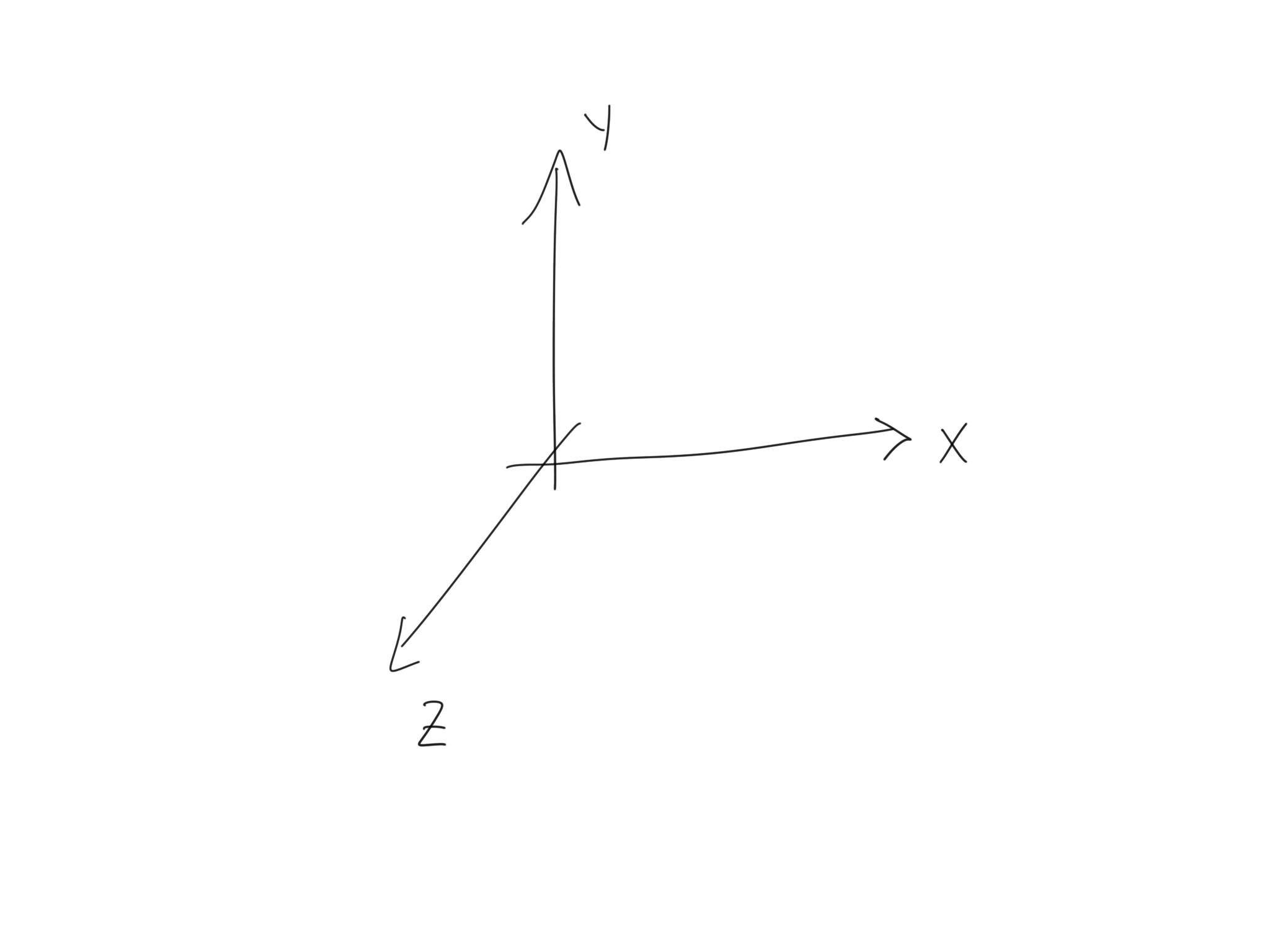
Ein kartesisches Koordinatensystem gibt es auch mit drei Achsen. Wir können es verwenden, um Punkte im Raum zu beschreiben.
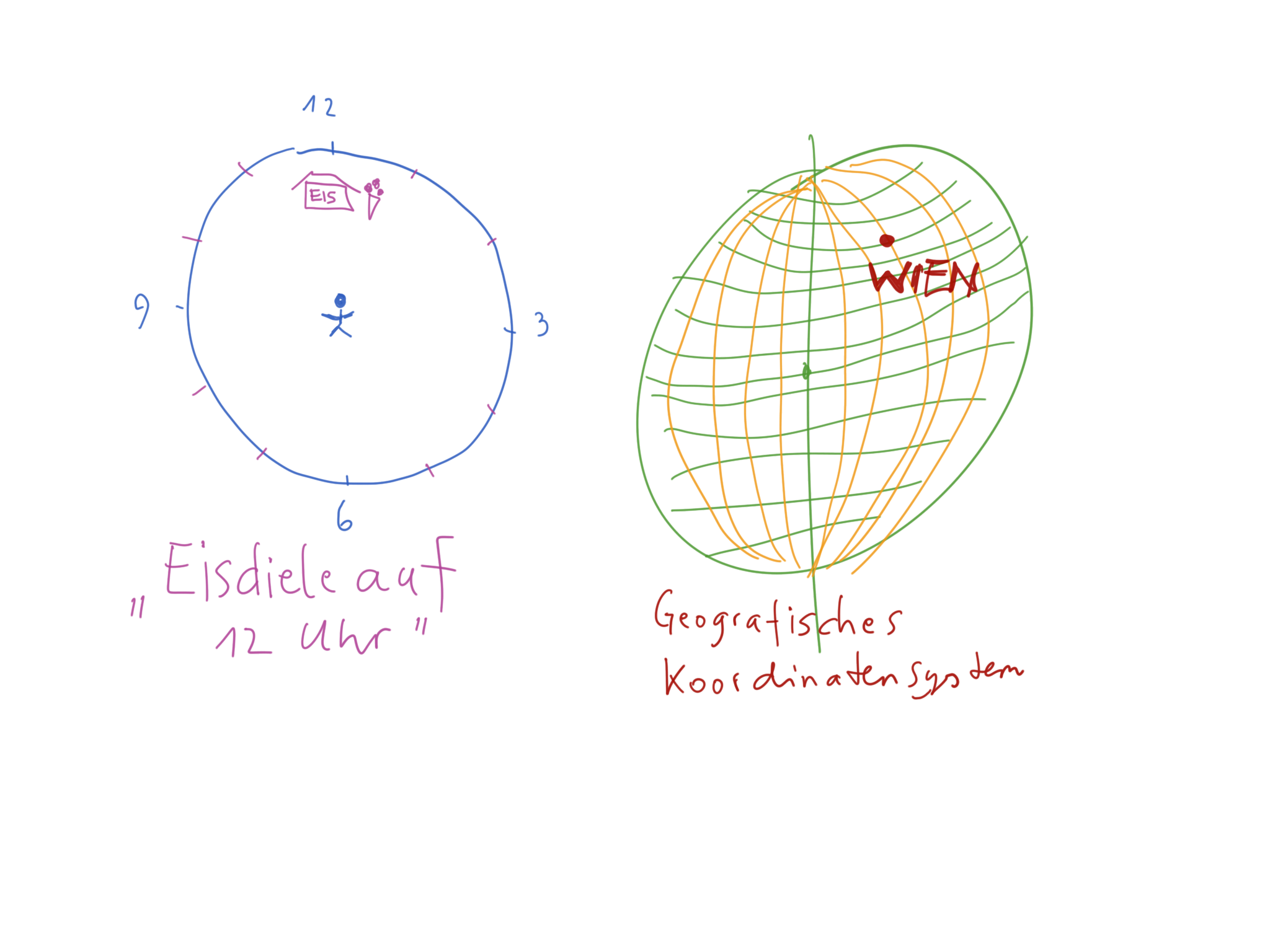
Es gibt noch viele weitere Koordinatensysteme, je nach Bedarf. Vielleicht kennen Sie auch diese zwei Koordinatensysteme:
Selbst für Menschen und Tiere gibt es Koordinatensysteme. (Foto: Ingrid Rachbauer)
Anatomische Lage- und Richtungsbezeichnungen helfen zum Beispiel, die Positionen der schwarzen Flecken auf dem Pferd zu beschreiben. Sie werden das kennenlernen, wenn Sie Veterinärmedizin studieren.
3. Geometrische Übungen
Wer das kartesische Koordinatensystem kennt, kann die folgenden Übungen machen.
Wörter 2
https://www.phyx.at/wp-content/uploads/2017/06/m116w2-a.mp3
der Zug, die Strecke, der Streckenzug, tragen, eintragen, der Eintrag, binden, verbinden, zeichnen, einzeichnen, die Gerade, der Punkt, parallel, laufen, sich verlaufen (Alltag), verlaufen (Mathematik), schneiden, der Schnitt, der Schnittpunkt, der Abstand, die Mitte, der Mittelpunkt, der Radius, die Tangente, berühren, die Berührung, der Berührpunkt / der Berührungspunkt
Streckenzug
Zeichnen Sie die folgenden Punkte in ein Koordinatensystem ein. Verbinden Sie die Punkte von A bis G. Wir sagen dazu „Streckenzug“ oder „Polygonzug“.
A (−4|−6), B (−4|0), C (−2|2), D (0|−2), E (2|2), F (4|0), G (4|−6)
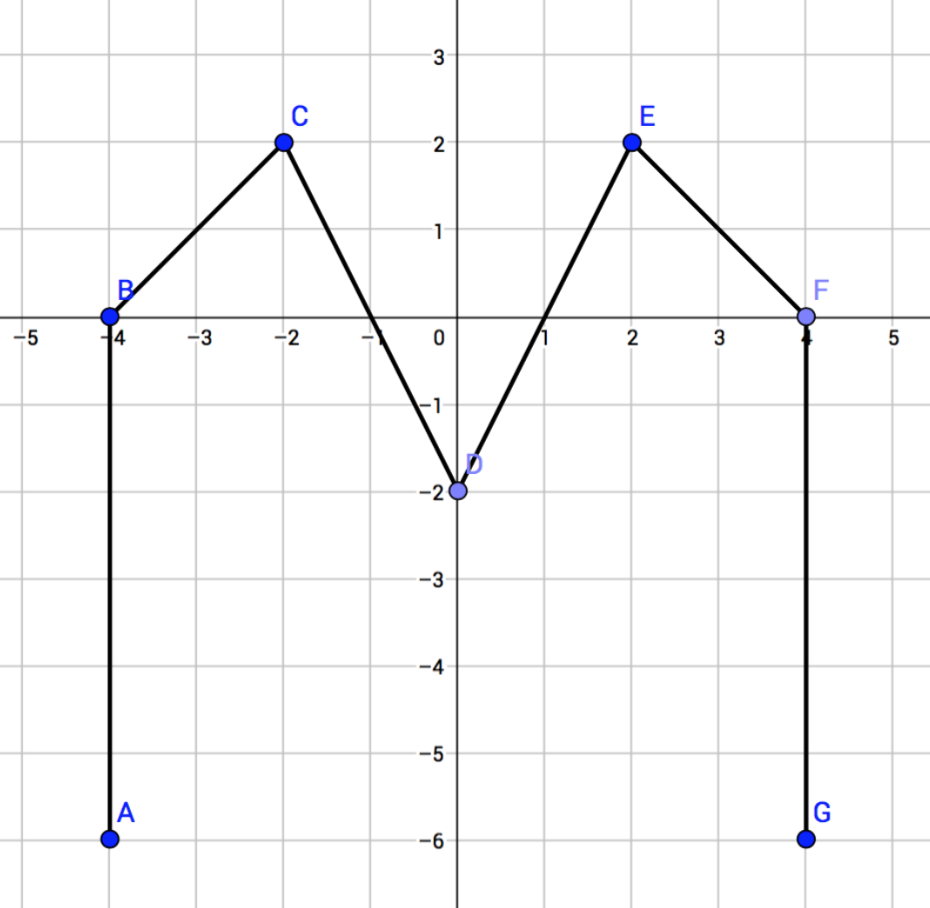
Gerade
Zeichnen Sie eine Gerade durch die Punkte R (0|0) und S (5|5).
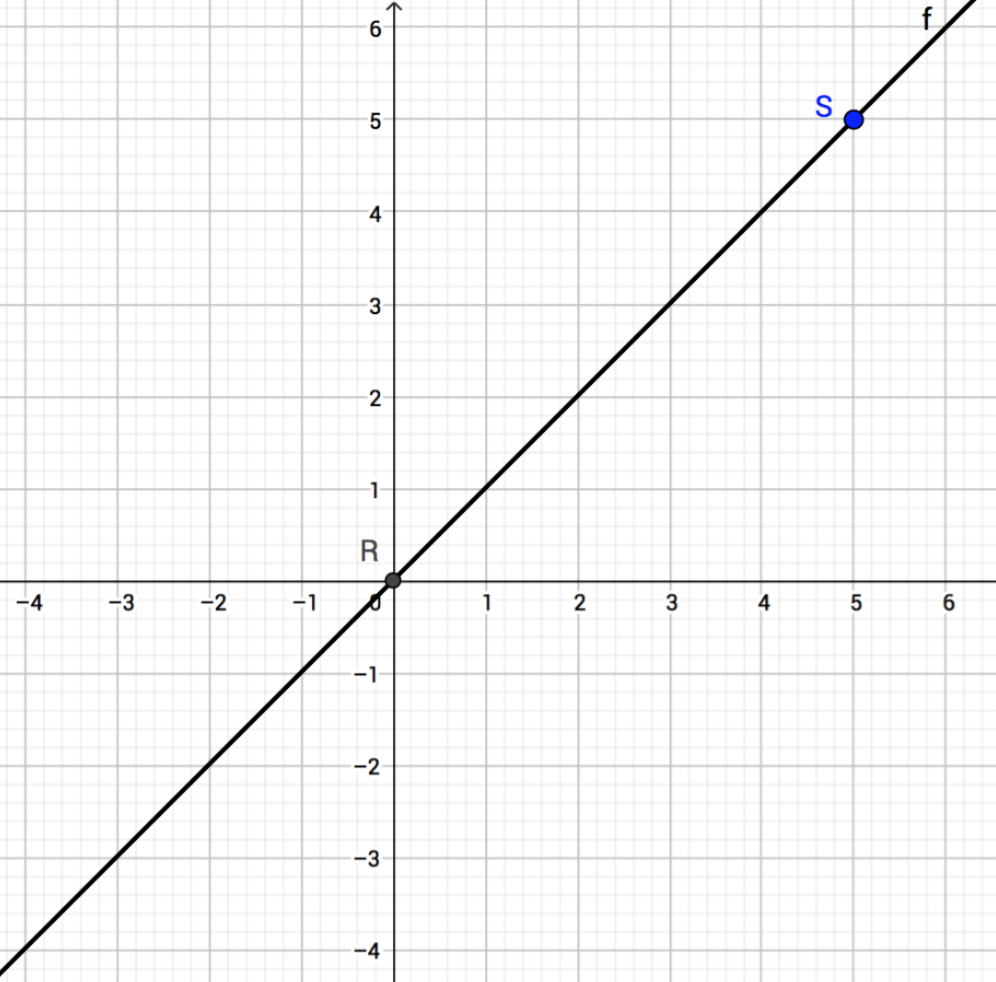
Parallele Gerade
Zeichnen Sie eine Gerade durch die Punkte U (−2|1) und V (4|−1). Zeichnen Sie eine zweite Gerade, die parallel ist und durch den Punkt W (2|1) verläuft.
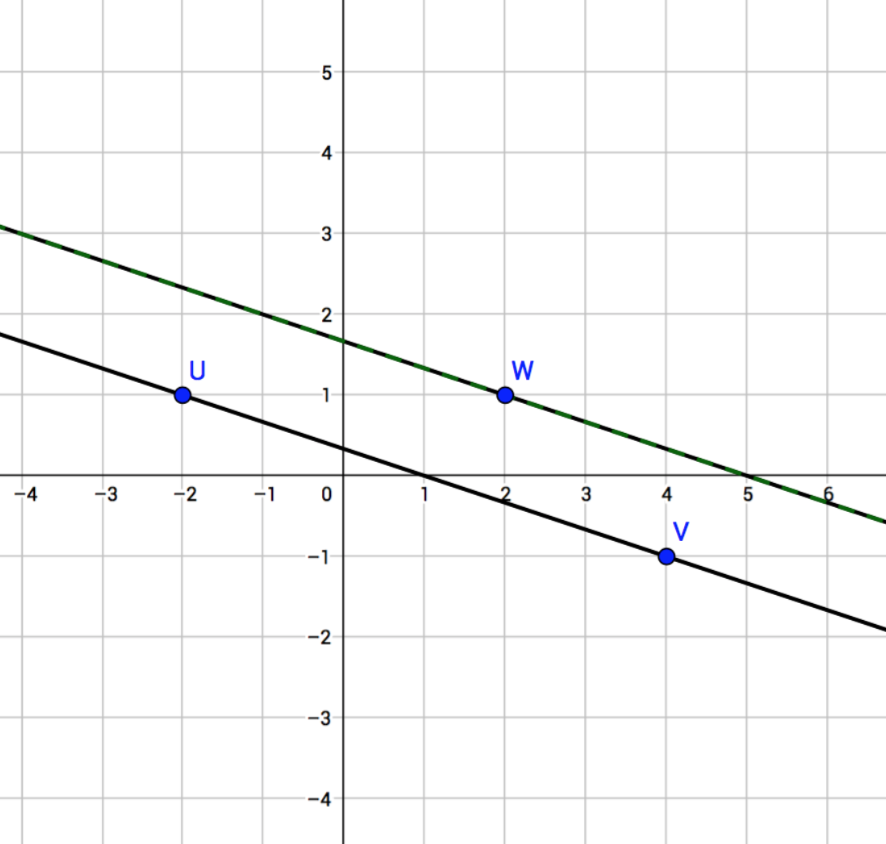
Senkrechte Gerade
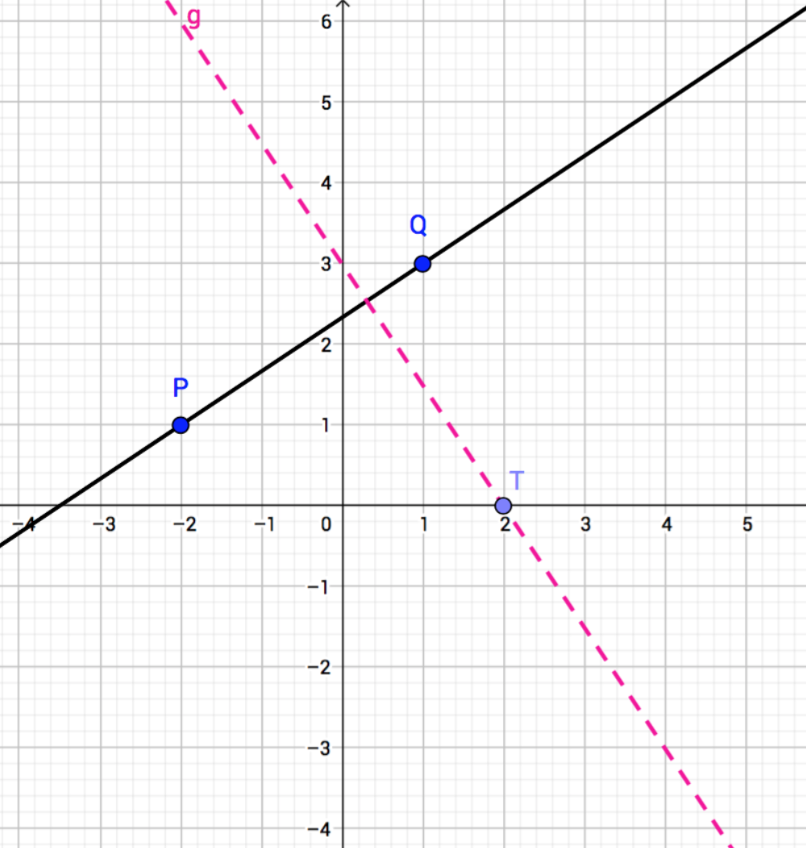
Zeichnen Sie eine Gerade durch die Punkte P (−2|1) und Q (1|3). Zeichnen Sie eine zweite Gerade, die senkrecht dazu ist und durch den Punkt T (2|0) verläuft.
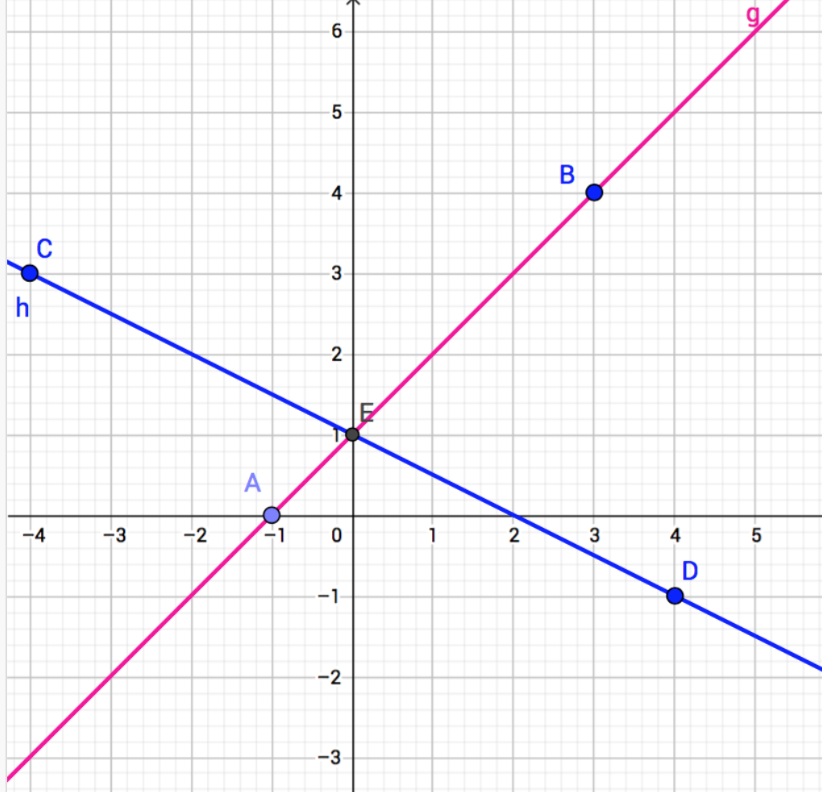
Schnittpunkt
Zeichnen Sie die beiden Geraden und bestimmen Sie den Schnittpunkt S.
g: [A (0|−1), B (3|4)] und h: [C (−4|3), D (4|−1)]
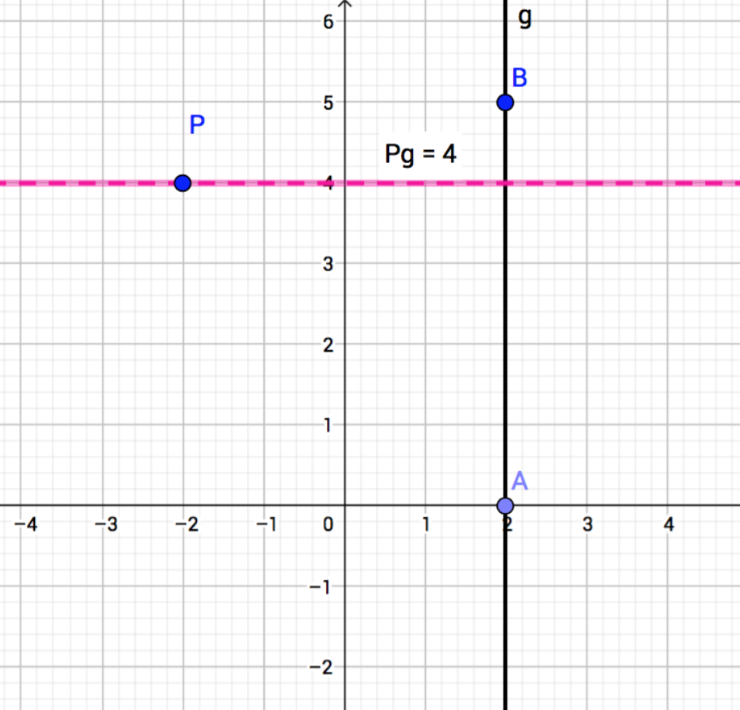
Abstand
Zeichnen Sie eine Gerade g durch die Punkte A (2|0) und B (2|5). Wie groß ist der Abstand des Punktes P (−2|4) von der Geraden?
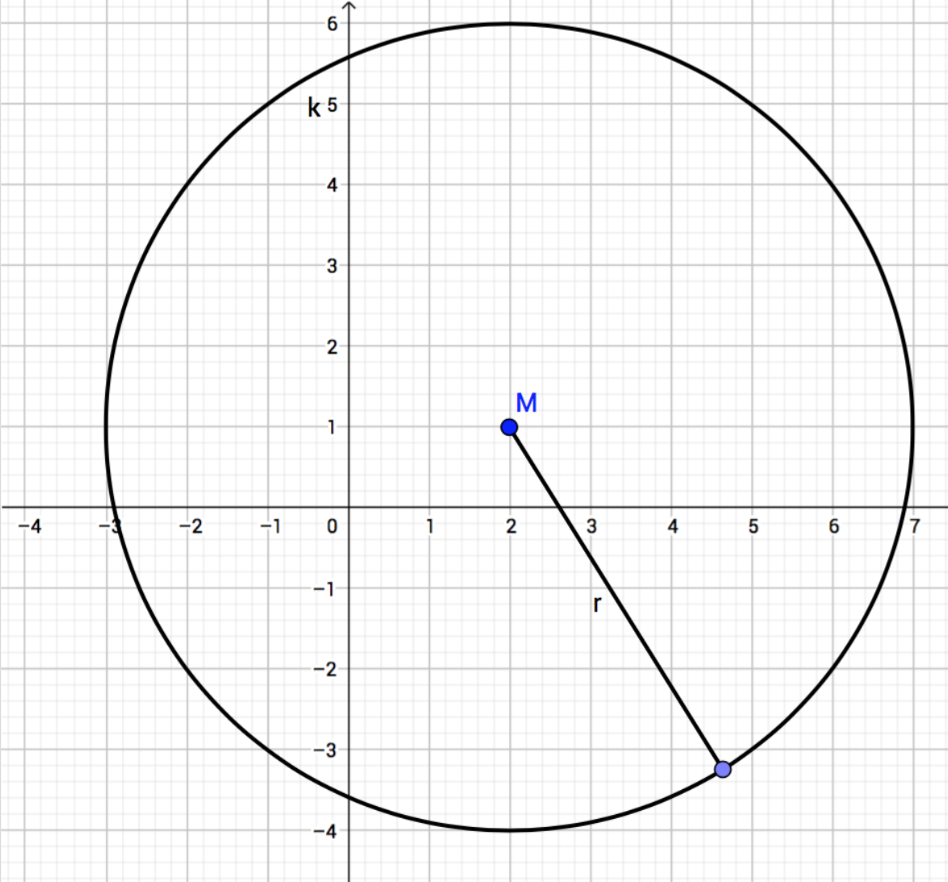
Kreis
Zeichnen Sie einen Kreis. Sein Mittelpunkt M ist in (2|1). Sein Radius soll r = 5 cm sein.
Kreis und Gerade
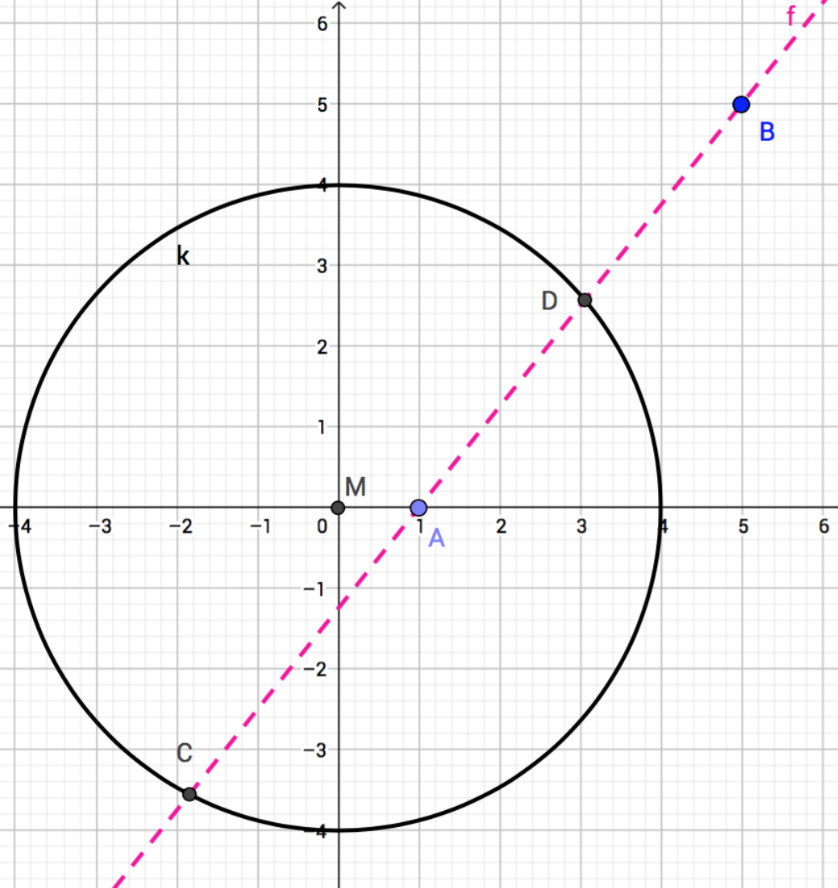
Zeichnen Sie einen Kreis. Sein Mittelpunkt M ist in (0|0). Sein Radius soll r = 4 cm sein. Zeichnen Sie nun eine Gerade durch die Punkte A (1|1) und B (5|5). Geben Sie die Schnittpunkte C und D von Kreis und Gerader an.
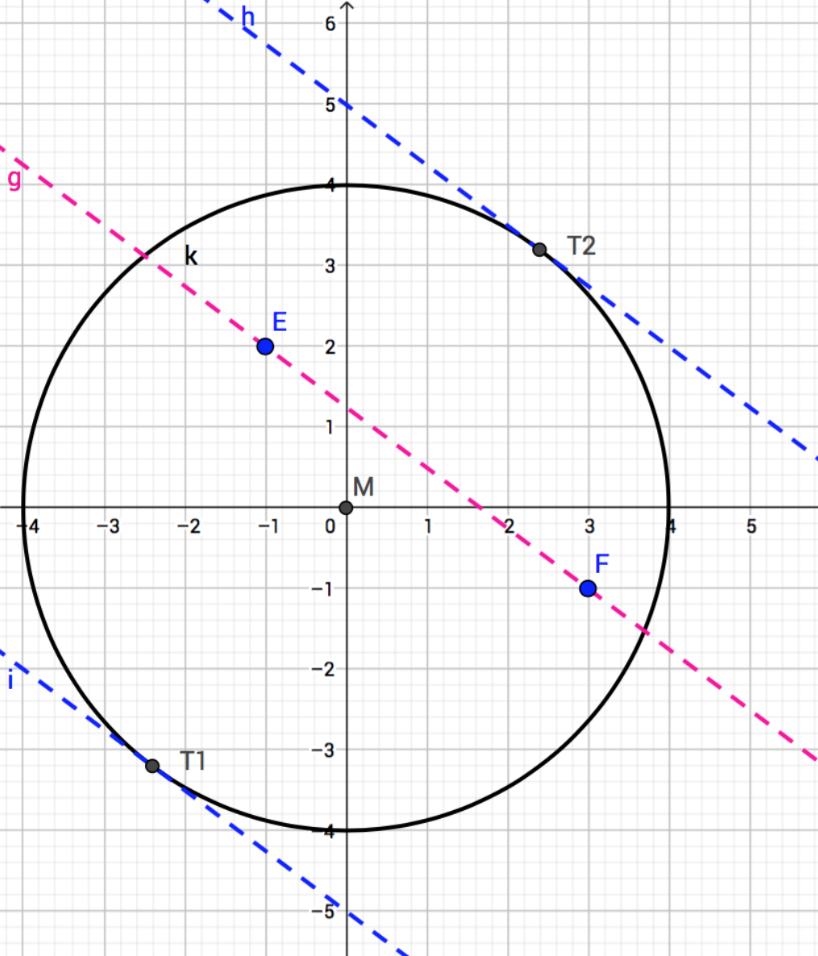
Kreis, Gerade, Tangenten
Zeichnen Sie einen Kreis. Sein Mittelpunkt M ist in (0|0). Sein Radius soll r = 4 cm sein. Zeichnen Sie nun eine Gerade g durch die Punkte E (−1|2) und F (3|−1). Zeichnen Sie die beiden Geraden, die zu g parallel sind und den Kreis berühren. Sie werden Tangenten genannt. Geben Sie die Koordinaten der Berührungspunkte an.
4. Praktisch und gut
Wenn Sie schnell und schön am Bildschirm geometrische Aufgaben bearbeiten möchten, dann können Sie das mit GeoGebra tun. Probieren Sie das doch für dieses Kapitel mit den obigen Beispielen aus.
Das war’s für dieses Mal. Bis zum nächsten Kapitel alles Liebe.