Wörter 1
die Zahl, die Reise, beginnen, der Beginn, die Welt, die Mathematik, die Art, die Zahlenart, unterscheiden, der Unterschied, bestimmen, gehen, der Bürgermeister, besuchen, der Besuch, die Familie, das Haus, die Mutter, zuhause, das Kind, alt, das Alter, multiplizieren, das Produkt, die Weile, sagen, eindeutig, der Tipp, zusammenzählen, die Summe, die Nummer, das Haus, die Hausnummer, die Älteste, das Spiel, Schach, das Schachspiel, nicken, klar, die Quelle, versuchen, zuerst, möglich, die Kombination, die Alterskombination, verwenden, die Verwendung, natürlich, natürliche Zahlen, das Komma, die Folge, die Reihenfolge, unwesentlich, das Gleiche, brauchen, schreiben, aufschreiben, das Kriterium, auffallen, stecken, der Satz, die Information
1. Aufgabe
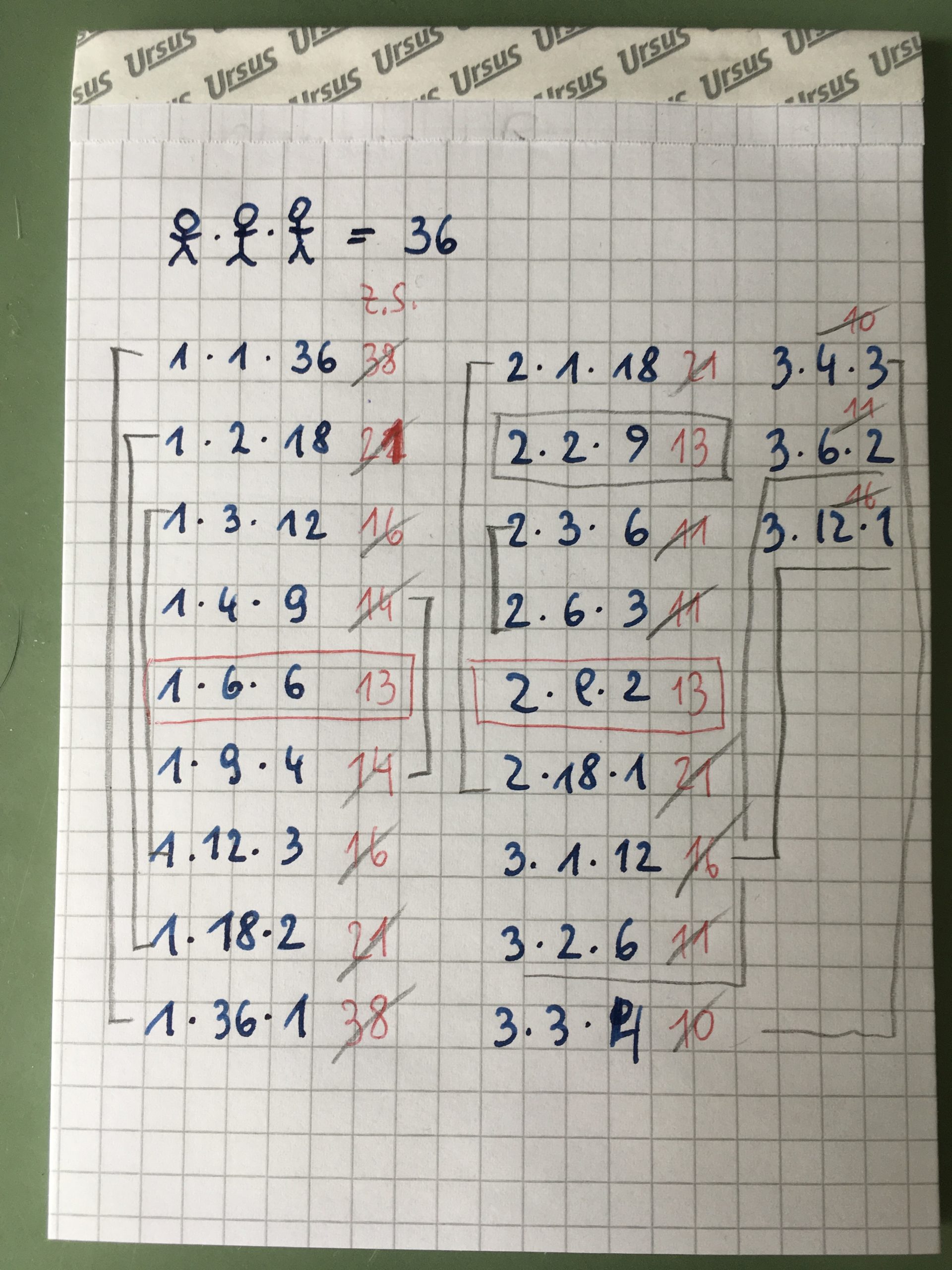
Der Bürgermeister besucht eine Familie in ihrem Haus. Die Mutter ist zuhause. „Wir haben drei Kinder“, sagt sie. „Wie alt sind Ihre Kinder?“, fragt der Bürgermeister. Wenn sie das Alter der drei Kinder multiplizieren, ist das Produkt 36. „Oh“, sagt der Bürgermeister nach einer Weile, „das ist nicht eindeutig. Können Sie mir einen weiteren Tipp geben?“. „Ja“, sagt die Mutter. „Wenn Sie das Alter der drei Kinder zusammenzählen, ergibt die Summe unsere Hausnummer.“ „Oh“, sagt der Bürgermeister nach einer Weile, „das ist immer noch nicht eindeutig. Können Sie mir noch einen Tipp geben?“. „Ja“, sagt die Mutter“. „Die Älteste spielt Schach“. Der Bürgermeister nickt. Jetzt ist alles klar. – Quelle: Simon Singh, Parallel Project
Wie alt sind die Kinder?
Hilfe 1 (Spoiler)
Hilfe 2 (Spoiler)
Hilfe 3 (Spoiler)
Lösung
Die Kinder sind 2, 2, und 9 Jahre alt. Warum? Es gibt zwei Kombinationen mit der Hausnummer 13: 1/6/6 und 2/2/9. Nur die zweite Kombination hat ein ältestes Kind. In diesem Film zeigen wir Ihnen im Detail, wie wir das Problem gelöst haben.
Kurfassung ohne Video:
2. Die natürlichen Zahlen
Das Alter von Menschen wird in Jahren gezählt. Immer wenn wir etwas zählen, verwenden wir dafür die „einfachsten Zahlen“: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 und so weiter. Es gibt unendlich viele dieser Zahlen. Wir nennen sie natürliche Zahlen und schreiben kurz:
Wörter 2
das Alter, zählen, immer, etwas, verwenden, die Verwendung, einfach/einfacher/am einfachsten, natürlich, die Anzahl, das Mögliche, zählen, das Gezählte, das Komma, halb, sortieren, die Größe, wieder, die Vermutung, richtig, falsch, erinnern, die Erinnerung, die Temperatur, unter, kälter, das Thermometer, zeigen, die Lösung, das Problem, die Null, die Geschichte
- Mit natürlichen Zahlen können Sie das Alter von Menschen angeben.
- Mit natürlichen Zahlen können Sie die Anzahl Ihrer Freunde angeben.
- Mit natürlichen Zahlen können Sie alles Mögliche zählen.
- Natürliche Zahlen haben kein Komma. Es gibt keine halben natürlichen Zahlen.
Beobachtungen
- Wir können die natürlichen Zahlen der Größe nach sortieren: 0 < 1 < 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9 < …
- Wenn wir natürliche Zahlen addieren, dann erhalten wir wieder eine natürliche Zahl: 13 + 6 = 19
- Wenn wir natürliche Zahlen multiplizieren, dann erhalten wir wieder eine natürliche Zahl: 2 • 9 = 18
Vermutung
Wenn wir natürliche Zahlen subtrahieren, erhalten wir wieder eine natürliche Zahl?
17 – 6 = 11 … die Vermutung ist richtig.
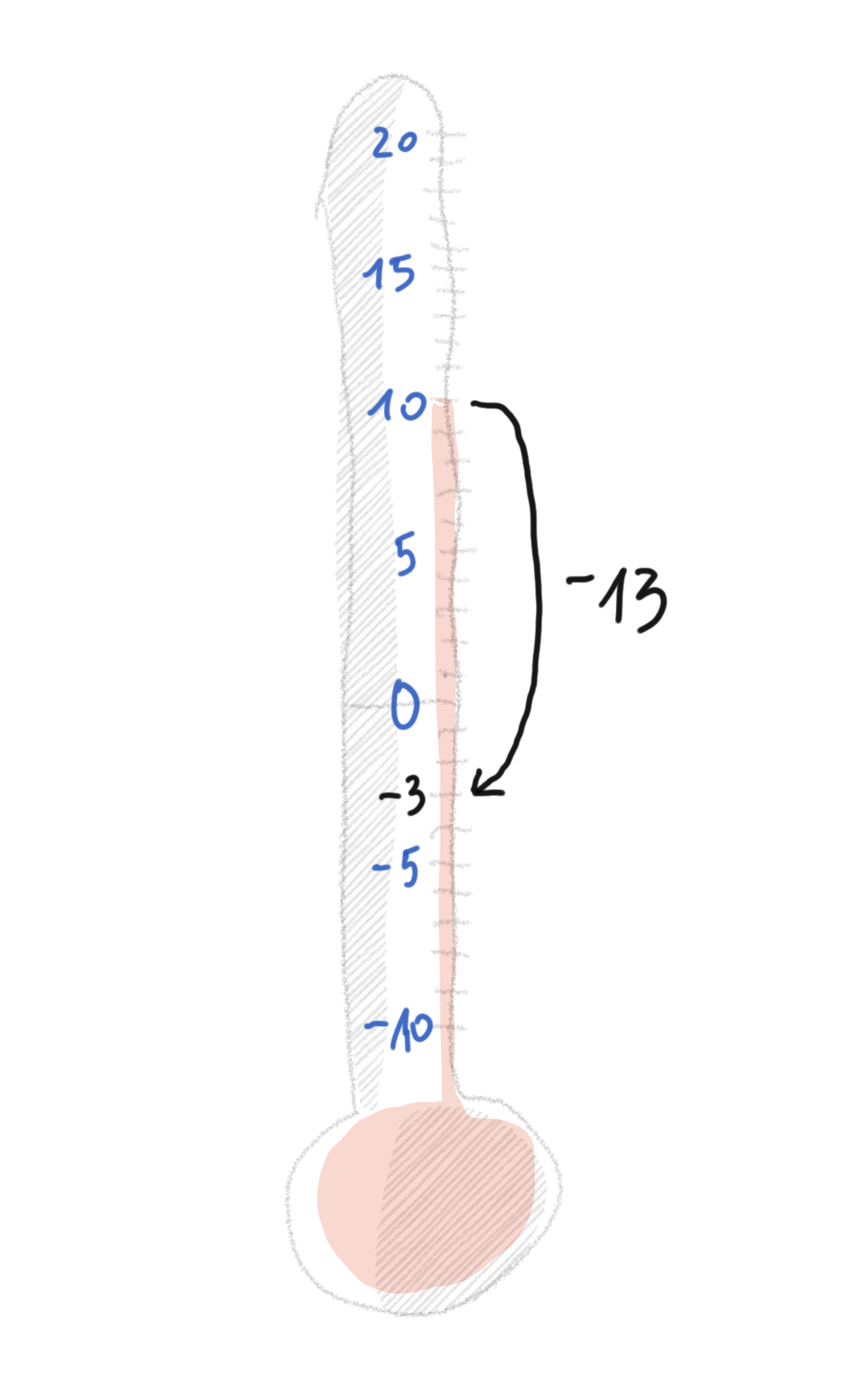
10 – 13 = ? … die Vermutung ist falsch. Es gibt keine natürlichen Zahlen unter 0.
Wir erinnern uns
Es gibt eine Temperatur unter 0. Es hat 10 Grad, und es wird um 13° kälter. Das Thermometer zeigt die Lösungen des Problems: Es hat –3°.
3. Die Ganzen Zahlen
Es gibt Temperaturen unter Null: diese Temperaturwerte haben ein – als Vorzeichen.
Beispiel:
Wir sagen: –3 hat ein negatives Vorzeichen. –3 ist eine negative Zahl.
Wörter 3
ganz, der Wert, die Temperatur, der Temperaturwert, das Zeichen, das Vorzeichen, negativ, erweitern, die Erweiterung, das Stück, das Gegenstück, kommen, dazukommen, groß/größer/am größten, die Menge, die Zahlenmenge, neben, finden, das Komma, nennen, schreiben, kurz, anders, sortieren, der Betrag, ausborgen, die Bilanz, schreiben, halb, beobachten, die Beobachtung, vermuten, die Vermutung, der Bruch, die Bruchzahl, die Dezimalzahl, die Kommazahl, der Taschenrechner, erinnern, die Erinnerung, bekommen, drei Viertel, die Pizza
Wir erweitern die natürlichen Zahlen um ihre „negativen Gegenstücke“: zu 1 kommt –1, zu 2 kommt –2, zu 3 kommt –3, zu 4 kommt –4, zu 5 kommt – 5, und so weiter.
Wir sprechen: Minus Eins. Minus Zwei. Minus Drei. Minus 4. Minus 5.
Wir sprechen: – ist das negative Vorzeichen.
So erhalten wir eine größere Zahlenmenge, in der neben allen natürlichen Zahlen auch ihre negativen Gegenstücke zu finden sind. Aber keine Kommas. Wir nennen diese Menge ganze Zahlen und schreiben kurz:
={0, 1, –1, 2, –2, 3, –3, …}
Anders sortiert:
={–3, –2, –1, 0, 1, 2, 3, …}
- Mit ganzen Zahlen können Sie Temperaturen angeben.
- Mit ganzen Zahlen können Sie sich auch €-Beträge ausborgen.
- Mit ganzen Zahlen können Sie Bilanzen schreiben.
- Ganze Zahlen haben kein Komma. Es gibt keine halben ganzen Zahlen.
Beobachtungen
- Die Ganzen Zahlen können wir der Größe nach sortieren. Wir beginnen bei „ganz kalt“:
… < –9 < –8 < –7 <–6 <–5 <–4 <–3 <–2 < –1 < 0 < 1 < 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9 < … - Wenn wir ganze Zahl addieren, erhalten wir wieder eine ganze Zahl: –9 + 3 + 7 = 1
- Wenn wir ganze Zahl multiplizieren, erhalten wir wieder eine ganze Zahl: –2 • 2 = –4
- Wenn wir ganze Zahl subtrahieren, erhalten wir wieder eine ganze Zahl: –8 – 10 = –18
- Alle natürlichen Zahlen (+) sind auch ganze Zahlen (+ und –)
Vermutung
Wenn wir ganze Zahlen dividieren, erhalten wir wieder eine Ganze Zahl?
20 / 5 = 4 … die Vermutung ist richtig; (wir schreiben auch 20 : 5 = 4)
–18 / 3 = –6 … die Vermutung ist richtig; (wir schreiben auch –18 : 3 = –6)
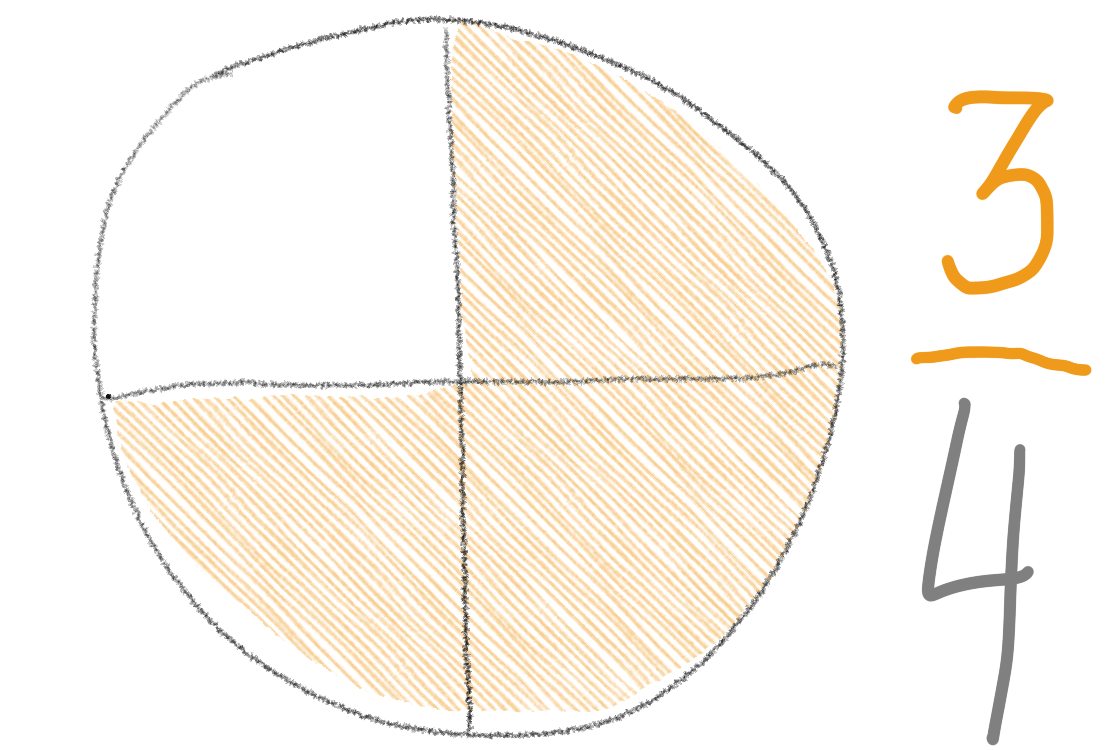
3 / 4 = … die Vermutung ist falsch. Das ist keine ganze Zahl.
3 / 4 ist eine Bruchzahl. Sprich: Drei Viertel. Wenn wir Drei durch Vier mit dem Taschenrechner dividieren, erscheint 0,75. Das ist eine Dezimalzahl, eine Kommazahl. Das ist keine ganze Zahl.
Wir erinnern uns
Wir kennen das von der Pizza. 3 / 4 bedeutet: Du bekommst drei von vier Stück. Oder:Drei Viertel von der Pizza gehört dir.
4. Die Bruchzahlen
Wörter 4
kombinieren, die Kombination, der Strich, der Bruchstrich, die Bruchzahl, oben, zählen, der Zähler, unten, nennen, der Nenner, das Zeichen, die Division, das Divisionszeichen, meist, die Menge, positiv, negativ, sortieren, die Größe, gleichzeitig, lernen, später, der Fall, das Spezielle, der Spezialfall, irrational, irrationale Zahlen, reell, reelle Zahlen, darstellen, darstellbar, die Darstellung
Wir kombinieren eine Ganze Zahl und eine Natürliche Zahl mit einem Bruchstrich zu einer Bruchzahl.
Beispiele für Bruchzahlen:
,
,
Die Zahl oben wird Zähler bezeichnet. Sie kann + positiv oder – negativ sein. Eine ganze Zahl.
Die Zahl unten wird Nenner bezeichnet. Sie gibt die Art des Bruches an und ist immer + positiv. Eine natürliche Zahl.
Ein Bruchstrich ist immer auch ein Divisionszeichen. Sie können jederzeit 3 : 4 berechnen, und erhalten meist eine Dezimalzahl – eine Zahl mit Komma. Dezimalzahlen sind Bruchzahlen.
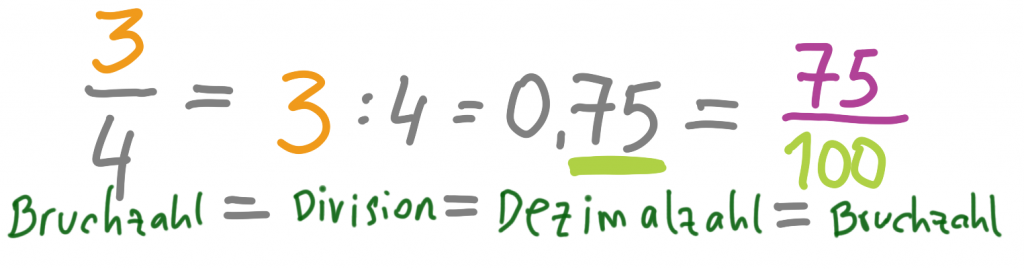
Wir schreiben die Menge aller Bruchzahlen auch so auf:
m … Ganze Zahl (da kannn schon mal ein – dabei sein)
n … Natürliche Zahl (immer positiv)
Wir lernen in einem späteren Kapitel, mit Bruchzahlen richtig zu rechnen.
Beobachtungen
Bruchzahlen sortieren
,
,
Was ist größer, was ist kleiner? Wir können Bruchzahlen nicht sofort nach ihrer Größe sortieren. Wir müssen die Brüche zuerst zu Dezimalzahlen machen, indem wir sie dividieren. Diese Dezimalzahlen können wir der Größe nach ordnen.
und
und
–2 < 0,75 < 0,8
Daher:
Bruchzahlen addieren
Wenn wir Bruchzahlen addieren, dann erhalten wir wieder eine Bruchtzahl:
Bruchzahlen subtrahieren
Wenn wir Bruchzahlen subtrahieren, dann erhalten wir wieder eine Bruchzahl
Bruchzahlen multiplizieren
Wenn wir Bruchzahlen multiplizieren, dann erhalten wir wieder eine Bruchzahl:
h4>Bruchzahlen dividieren
Wenn wir Bruchzahlen dividieren, dann erhalten wir wieder eine Bruchzahl:
Wir lernen das im Detail noch später.
Beispiele
Zusammenfassung
Mit den Bruchzahlen kennen wir nun auch die Dezimalzahlen. Dezimalzahlen sind Bruchzahlen. Wir brauchen dazu nur die Brüche zu dividieren.
Wir kennen nun fast alle „Zahlen unseres Lebens“.
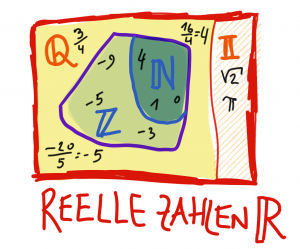 Wir werden später lernen, dass es auch Dezimalzahlen gibt, die wir nicht aus der Division einer Bruchzahlen erhalten. Sie heißen irrationale Zahlen, abgekürzt:
Wir werden später lernen, dass es auch Dezimalzahlen gibt, die wir nicht aus der Division einer Bruchzahlen erhalten. Sie heißen irrationale Zahlen, abgekürzt: . Zum Beispiel
oder
.
All das lernen wir noch etwas später. Diese Spezialfälle bilden mit den Bruch-Dezimalzahlen gemeinsam die Menge der Reellen Zahlen. Das sind alle für uns denkbaren Zahlen, mit denen wir üblicherweise arbeiten. Wir kürzen diese Zahlenmenge mit ab.
Alle natürlichen Zahlen sind auch ganze Zahlen, diese sind auch Bruchzahlen, und diese sind auch reelle Zahlen. Wir schreiben:
.
… Natürliche Zahlen (ohne Komma, + positiv)
Beispiele: 8, 20, 33, 100, 221
… Ganze Zahlen (ohne Komma, + positiv und – negativ)
Beispiele: –12, –5, 0, 7, 150
… Bruchzahlen (Rationale) Zahlen (+ positiv und – negativ;
; Dezimalzahlen)
Beispiele: ,
,
… Irrationale Zahlen (Nicht durch Bruch darstellbar, aber Dezimalzahlen)
Beispiele: ,
,
… Reelle Zahlen („Alle unsere Zahlen“)
Beispiele: –23,15, –3, 0, 4/3, , 5
Aufgaben
Zu welchen Zahlenmengen gehören die folgenden Zahlen?
1
Lösung
0
Lösung
-3
Lösung
Lösung
Lösung
Lösung
20,55
Lösung
Lösung
Lösung
5. Größer, kleiner oder gleich?
Setzen Sie das Größer- oder Kleinerzeichen richtig ein. Die Öffnung ist immer bei der großen Seite.
Wörter 5
größer, kleiner, gleich, das Zeichen, das Größerzeichen >, das Kleinerzeichen <, das Bild, gleich =, unbestimmt, die Masse, die Höhe, der Durchmesser
Beispiel

Lösung: >

Lösung: <
Übungen


Lösung


Lösung
Möglichkeit 1: Füllmenge in g (Gramm) – Erstes Bild: < Zweites Bild: >
Möglichkeit 2: Höhe der Dose – Erstes Bild: < Zweites Bild: >
Möglichkeit 3: Durchmesser der Dose – Erstes Bild: > Zweites Bild: <


Lösung


Lösung


Lösung


Lösung


Lösung


Lösung


Lösung


Lösung
Übungen
Ordnen Sie bitte diese Zahlen der Größe nach:
8, –5, 0, 2, –10
Lösung
–12, 3, –1, 7, -20
Lösung
–12, 3, –1, 7, -20
Lösung
20,03; 20,002; 21
Lösung
,
, 0,1
Lösung
0,1; 0,3; 0,5
0,1; ;
6. Rechnen mit + Plus und – Minus
Der Taschenrechner liefert gute Ergebnisse. Das ist in Ordnung. Besser ist es aber, auch ohne Taschenrechner die Ergebnisse zu verstehen.
Wörter 6
rechnen, + plus, – minus, der Taschenrechner, gut/besser/am besten, das Ergebnis, die Ordnung, ohne, verstehen, das Verständnis, nachdenken, überlegen, das Bild, das Thermometer, zeichnen, das Beispiel, gleich, ungleich, das Zeichen, das Vorzeichen
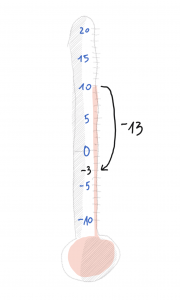
Addition und Subtraktion
Nachdenken und mit einem Bild vom Thermometer überlegen.
- Beispiel: 10 – 13 = –3
- Beispiel: –5 + 10 = +5
- Beispiel: –5 – 10 = –15
Übung
Zeichnen Sie ein Bild von einem Thermometer zum 2. und 3. Beispiel.
Multiplikation und Division
Gleiche Vorzeichen ergeben +
Ungleiche Vorzeichen ergeben –
+ • + = +
– • – = +
+ • – = –
– • + = –
- Beispiel: –5 • 10 = –5
- Beispiel: –5 • (–10) = +50
+ / + = +
– / – = +
+ / – = –
– / + = –
- Beispiel: –10 / 5 = –2
- Beispiel: –10 / (–5) = +2
Hinweise
- Statt +2 schreiben wir auch einfach 2.
- Statt 5 • –2 schreiben wir lieber 5 • (–2).
- + kann ein Rechenzeichen für die Addition sein, oder ein Vorzeichen.
5 +3 = (Rechenzeichen für die Addition)
+3 (Vorzeichen für die Zahl 3) - – kann ein Rechenzeichen für die Subtraktion sein, oder ein Vorzeichen.
5 – 3 = (Rechenzeichen für die Addition)
–3 (Vorzeichen für die Zahl Minus Drei)
Übungen:
Wörter 7
das Konto, der Kontostand, dazu kommen, hoch, einfach, die Temperatur, betragen, °Celsius (Grad Celsius), kalt/kälter/am kältesten, warm/wärmer/am wärmsten, heben, beheben, das Stück, der Schein
- Der Kontostand beträgt –200 €. Es kommen 500 € dazu. Wie hoch ist der Kontostand?
Lösung
+300 € oder einfach 300 € - Der Kontostand beträgt –100 €. Es kommen 300 € weg. Wie hoch ist der Kontostand?
Lösung
–400 € - Die Temperatur beträgt 4° Celsius. Es wird in der Nacht um 12° Celsius kälter. Wie kalt ist es in der Nacht?
Lösung
–8° Celsius - Die Temperatur beträgt am Morgen –2° Celsius. Es wird um 15° Celsius wärmer. Welche Temperatur hat es nun?
Lösung
+13° Celsius - Wieviel ist –50 • –2
Lösung
+100 oder einfach 100 - Wieviel ist 50 / (–2)
Lösung
-25 - Jemand hat 100 € auf seinem Konto. Er behebt 10 Stück 20 €-Scheine. Wie groß ist nun der Kontostand?
Lösung
-100 €
 7. Buchtipp
7. Buchtipp
Fermats letzter Satz: Die abenteuerliche Geschichte eines mathematischen Rätsels.
Das war’s für dieses Mal. Das war heute ein wenig länger. Die kommenden Kapitel sind dann wieder etwas kürzer. Schön, dass Sie mit dabei sind.
Fehler gefunden? Bitte schicken Sie ein E-Mail an fehler@phyx.at. Vielen Dank!




