Grundlagen der Mathematik 2 – Übungsaufgaben | Physikalische Soiree

Mein Kaktus kann Brüche

Mit diesen Aufgaben festigen Sie Ihr Wissen. Verwenden Sie auch Ihre Lernunterlagen, wenn es Probleme gibt. Die Lösungen finden Sie bei den Beispielen. Gerne können Sie ganz unten auch kommentieren wenn Sie Fragen haben, oder wenn Sie einen Fehler finden. Wenn Sie auch Mathematik 1 wiederholen möchten, dann bitte hier entlang.

Und hier sind die Aufgaben:

M201: Zahlen den Zahlenmengen zuordnen

Wiederholung mit Übungsaufgaben: https://www.phyx.at/mathematik/m1/m04/
Erklären Sie bitte die Zahlenmengen $\mathbb{N}, \mathbb{Z}, \mathbb{Q},\mathbb{I}, \mathbb{R}$
Welchen Zahlenmenge ist die Dezimalzahlen 0,45 zuzordnen?

Lösungen

2. Aufgabe

$\mathbb{N}$ Menge der natürlichen Zahlen (keine Kommastellen, positiv)

$\mathbb{Z}$ Menge der ganzen Zahlen (keine Kommastellen, positiv und negativ)

$\mathbb{Q}$ Menge der Bruchzahlen (Rationale Zahlen, Zahl ohne Kommastelle / Zahl ohne Kommastelle; positiv und negativ, alle Deziamlzahlen (Kommazahlen) sind ebenso Bruchzahlen, wenn sie nicht unendlich viele Kommastellen haben)

$\mathbb{I}$ Menge der irrationale Zahlen (Zahlen, die man nicht als Dezimalzahlen mit endlich vielen Kommastellen darstellen kann, positiv und negativ)

$\mathbb{R}$ Menge der reellen Zahlen (Rationale und irrationale Zahlen zusammen, positiv und negativ, also „alle“ Zahlen, mit denen wir arbeiten)

3. Aufgabe

0,45 ist eine rationale Zahl, denn

$0,45=\dfrac{45}{100}$

M202: Rechengesetze für Potenzen

Berechnen Sie bitte
$a+a+a=$
$a \cdot a \cdot a \cdot a=$
$ab+3ab+2ab-ab^2=$
Berechnen Sie bitte
$a^5 \cdot a^3 \cdot a^9=$
$\dfrac {a^2}{a^5} \cdot a^2=$
$\dfrac {a^{-2}}{a^{-5}} \cdot a^2=$
$a^0+a^1=$
Die Rechengesetzte: Wie werden Potenzen gleicher Basen multipliziert und dividiert, wie werden Potenzen potenziert?
Jetzt noch diese Übungsaufgaben Potenzrechnen zum Zusammenfassen
Möchten Sie dieses Thema perfektionieren? Das könnten Sie mit diesen Aufgaben tun.

Lösungen

1. Aufgabe

$3a$

$a^4$

$6ab-ab^2$

2. Aufgabe

$a^{17}$

$\dfrac {1}{a}=a^{-1}$

$\dfrac {1}{a^{-5}}=a^5$

$1+a$

3. Aufgabe

Potenzen gleicher Basen werden multipliziert, indem man ihre Exponenten addiert. Potenzen gleicher Basen werden dividiert, indem man ihre Exponenten subtrahiert. Potenzen werden potenziert, in dem man die Exponenten multipliziert.

M203: Potenzen mit rationalen Exponenten (Wurzeln)

Wandeln Sie bitte die Pozenz in Wurzelschreibweise um
$a^{1/2}=$
$a^{3/2}=$
$a^{3/5}=$
Berechnen Sie bitte
$a^{3/2} \cdot a^{2/3} \cdot a^{-1}=$
$\dfrac {a^{3/2}}{a^{5/2}} \cdot a^2=$
$\dfrac {a^{-{3/2}}}{a^{5}} \cdot a^{-3/2}=$
Wandeln Sie bitte die Wurzel in Potenzschreibweise um
$\sqrt [3]{a}=$
$\sqrt [2]{a^5}=$
$\sqrt [3]{a^{-2}}=$

Lösungen

1. Aufgabe

$\sqrt {a}$

$\sqrt {a^3}$

$\sqrt [5]{a^3}$

2. Aufgabe

$a^{\frac{7}{6}}$

$a$

$a^{-8}$

3. Aufgabe

$a^{\frac{1}{3}}$

$a^{\frac{5}{2}}$

$a^{-\frac{2}{3}}$

M204: Rechnen mit Wurzeln: Zahlen und Terme “in” und “aus” einer Wurzel bringen

Verbinden Sie bitte die Wurzeln
$\sqrt [3]{a} \cdot \sqrt [3]{a^2}=$
Bringen Sie bitte die Zahl in die Wurzel
$3 \cdot \sqrt [2]{a}=$
Bringen Sie bitte die Zahl aus der Wurzel
$3 \cdot \sqrt [2]{16 \cdot a}=$

Lösungen

1. Aufgabe

$a$

2. Aufgabe

$\sqrt [2]{9a}$

3. Aufgabe

$12 \cdot \sqrt {a}$

Hinweis: wir schreiben statt $\sqrt [2]{a}$ auch einfach $\sqrt {a}$ .

M205: Dekadisches Zahlensystem, Gleitkommadarstellung, Abkürzungen

Formen Sie bitte in Gleitkommadarstellung um
6270=
0,0045=
150 Millionen=
Wie ist das dekadische Zahlensystem aufgebaut? Wiederholen Sie bitte hier.
Was bedeuten die Vorsilben „Mega-“ und „Milli-“ in Potenzschreibweise?

Lösungen

1. Aufgabe

$6,27 \cdot 10^3$

$4,5 \cdot 10^{-3}$

$1,5 \cdot 10^8$

3. Aufgabe

$10^6$

$10^{-3}$

Zwischendurch ein wenig tüfteln? Das ist ein hübsches Beispiel, das Sie mit Hausverstand und etwas Wissen über Prozente sicher lösen können. Überraschendes Ergebnis.

Lösung

100 rote Kerzen müssen verbrannt werden.

M206: Einfache Textbeispiele überschlagsmäßig und genau rechnen

Ein Hurrikan braucht drei Tage, um eine Strecke von 1200 km zurückzulegen. Wie groß ist seine Durchschnittsgeschwindigkeit? Rechnen Sie zuerst überschlagsmäßig, und dann genau.
Licht hat eine Geschwindigkeit von 300.000 km/s. Die Entfernung von der Sonne zur Erde ist 150 Millionen km. Wie lange braucht das Licht von der Sonne zur Erde? Rechnen Sie zuerst überschlagsmäßig, und dann genau.
Alle zwei Monate verdoppelt sich der Bitcoin-Kurs. Vorausgesetzt die Blase platzt nicht, und es geht so weiter: Wie lange dauert es ungefähr, bis aus 600 Euro 1 Million Euro geworden sind? Genau werden Sie das erst in späteren Mathekursen mit exponentiellen Funktionen rechnen.

Lösungen

1. Aufgabe

rund 20 km/h, genau 16,7 km/h

2. Aufgabe

rund 500 Sekunden, genau: 8 Minuten 20 Sekunden

3. Aufgabe

rund 22 Monate. Aber die Blase wird vorher platzen.

M207: Potenzen in Termen vereinfachen, herausheben und ausmultiplizieren

Lösen Sie bitte die Klammern auf
$14-(3r-2)+(6r-7)=$
$(3s-4t)-(s-5t)+(t-2s)=$
Vereinfachen Sie bitte durch Ausmultiplizieren
$-2a^2(4a^3+5a+1)=$
$3a(5a+3)-5a(2a+1)=$
$(3a-2)(5a+4)-(6a+4)(2a-1)=$
Vereinfachen Sie bitte durch Herausheben
$24a^2-20a=$
$4a^3b-12a^2b^2=$
Möchten Sie dieses Thema perfektionieren? Weitere Aufgaben finden Sie im (dünnen) Buch auf Seite 11: Beispiele 83, 84, 85, 86, 87, 88, 89

Lösungen

1. Aufgabe

$9+3r$

$2t$

2. Aufgabe

$-8a^5-10a^3-2a^2$

$5a^2+4a$

$3a^2-4$

3. Aufgabe

$4a \cdot (6a-5)$

$4a^2b \cdot (a-3b)$

M208: Binomische Formeln

Berechnen Sie bitte auf zwei Arten: Ausmultiplizieren, und durch die Binomische Formel 1 und 2
$(7a+4)^2=$
$(6a-5)^2=$
$(x-6)^2=$
Schreiben Sie als Produkt, indem Sie die binomische Formel 1, 2 oder 3 anwenden
$9a^2-16=$
$x^2+12x+36=$
$4a^2-20ab+25b^2=$
Möchten Sie dieses Thema perfektionieren? Weitere Aufgaben finden Sie im (dünnen) Buch auf Seite 11: Beispiele 90 und 91

Lösungen

1. Aufgabe

$49a^2+56a+16$

$36a^2-60a+25$

$x^2-12x+36$

2. Aufgabe

$(3a-4) \cdot (3a+4)$

$(x+6)^2$

$(2a-5b)^2$

M209: Formeln umformen

Formen Sie bitte die physikalischen Formeln um

$E_{pot}=m \cdot g \cdot h$
$m=$
$g=$
$h=$
$E=mc^2$
$m=$
$c=$
$T=2 \pi \cdot \sqrt {\dfrac{l}{g}}=$
$g=$
$l=$

Lösungen

1. Aufgabe

$m= \dfrac{E_{pot}}{g \cdot h}$

$g= \dfrac{E_{pot}}{m \cdot h}$

$h= \dfrac{E_{pot}}{m \cdot g}$

2. Aufgabe

$m= \dfrac{E}{c^2}$

$c= \sqrt {\dfrac {E}{m}}$

3. Aufgabe

$l=g \cdot \left( \dfrac {T}{2\pi} \right) ^2$

$g= \dfrac {l}{\left( T/2 \pi \right) ^2}$

Mein anderer Kaktus kann auch Brüche

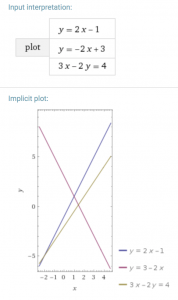
M210: Lineare Gleichungen

Lösen Sie bitte die Gleichung und rechnen Sie die Probe
$5x-13=47$
$46-16x=6$
$(3x+4)(2x-3)+8=2x(3x+2)$
Möchten Sie dieses Thema perfektionieren? Weitere Aufgaben finden Sie im (dünnen) Buch auf Seite 13: 104, 105, 106
Zeichnen Sie bitte die linearen Funktionen
$y=2x-1$
$y=-2x+3$
$3x-2y=4$
Lösen Sie bitte die folgenden linearen Textgleichungen
• Wenn man zum Drittel einer Zahl ein Viertel derselben Zahl addiert, erhält man 70.
• Gib zu einer Zahl zwei Drittel ihrer selbst hinzu und nimm vom Ergebnis ein Drittel weg, so bleibt 10.
• Der Umfang eines Rechtecks beträgt 30 cm. Die Länge ist um 3 cm länger als die Breite. Berechnen Sie die Seitenlängen.
• Möchten Sie dieses Thema perfektionieren? Weitere Aufgaben finden Sie unter diesem Link.

Lösungen

1. Aufgabe

$L=\left\{ 12 \right\}$

$L=\left\{ 2,5 \right\}$

$L=\left\{ - \dfrac{4}{5} \right\}$

2. Aufgabe

Klick zum Vergrößern, via wolframalpha.com: Eingabe plot (y=2x-1) and (y=-2x+3) and (3x-2y=4)

3. Aufgabe

Die Zahl lautet 120.

Die Zahl lautet 9.

$a=9$ , $b=6$

M211: Produkt-Null-Satz

Lösen Sie bitte die folgende Gleichung mit dem Produkt-Null-Satz
$(x-2)(x+3)=0$
Heben Sie bitte heraus und lösen Sie die Gleichung
$2x^2-x=0$
Umgekehrt zu Beispiel 1: Welche Gleichung hat folgende Lösungen
$x_1=5$
$x_2=-1$

Lösungen

1. Aufgabe

$L=\left\{ 2,-3 \right\}$

$L=\left\{ 0, \frac {1}{2} \right\}$

$(x-5)\cdot (x+1)$

$latex

M212: Bruchgleichungen

Bestimmen Sie Hauptnenner, Definitionsmenge und Lösung der Bruchgleichung
$\dfrac {4}{x-2}=\dfrac {3}{x-1}$

Lösung

$\text{Hauptnenner}=(x-2) \cdot (x-1)$

$D= \mathbb{R} \setminus \left\{ 1, 2 \right\}$

$L=\left\{ -2 \right\}$

M213: Quadratische Gleichungen

Lösen Sie bitte die quadratische Gleichung ohne Lösungsformel
$4x^2-9=0$
$2x^2+12=0$
$18x-3x^2=0$
Lösen Sie bitte die quadratische Gleichungen
$x^2+10x+24=0$
$x^2=8x-15$
$(x-5)^2+(2x+3)^2=(x+1)^2+97$
Möchten Sie das perfektionieren? Weitere Beispiele finden Sie hier.
Das Produkt zweier aufeinanderfolgenden Zahlen lautet 30. Berechnen Sie die beiden Zahlen.
Wie groß sind die Seiten eines Rechtecks, dessen Diagonale 25 cm lang und der Umfang 62 cm lang ist?
Möchten Sie das perfektionieren? Weitere Textaufgaben finden Sie hier.

Lösungen

1. Aufgabe

$L=\left\{ -\frac{3}{2},+\frac{3}{2} \right\}$

$L=\left\{ \right\}$

$L=\left\{ 0, 6 \right\}$

2. Aufgabe

$L=\left\{ -4, -6 \right\}$

$L=\left\{ 5, 3 \right\}$

$L=\left\{ -4, 4 \right\}$

4. Aufgabe

Die Zahlen lauten 5 und 6.

5. Aufgabe

Die Seiten lauten a=7 cm und b=24 cm.

M214: Lineare Gleichungssysteme

Lösen Sie das lineare Gleichungssystem rechnerisch und machen Sie die Probe
$I:2x+3y=7$
$II: 4x-y=7$
Lösen Sie das lineare Gleichungssystem rechnerisch und machen Sie die Probe
$I: 5x+3y=5$
$II: 12x+8y=14$
Lösen Sie das lineare Gleichungssystem rechnerisch und machen Sie die Probe
$I: 8x+17y=-1$
$II: 12x+11y=13$
Möchten Sie das perfektionieren? Sie finden weitere Beispiele im (dünnen Buch) auf Seite 15: 121-134

Lösungen

1. Aufgabe

$L=\left\{ (2,1) \right\}$

2. Aufgabe

$L=\left\{ (-\frac{1}{2},\frac{5}{2}) \right\}$

3. Aufgabe

$L=\left\{ (2,-1) \right\}$

M215: Lehrsatz des Pythagoras

Wie lautet der Satz des Pythagoras? Wo gilt dieser Satz? Bitte um eine Skizze.
Im rechtwinkeligen Dreieck: a=30 cm, b=40 cm. Wie groß ist die Hypothenuse c?
Berechnen Sie die Diagonale im Quadrat mit Seitenlänge a=30 cm.
Möchten Sie das perfektionieren? Sie finden weitere Übungsaufgaben hier.

Lösungen

1. Aufgabe

$a^2+b^2=c^2$

Der Satz des Pythagoras gilt im rechtwinkeligen Dreieck. a und b sind die Katheten – die kurzen Seiten. c ist die Hypotenuse – die lange Seite. Die Hypotenuse befindet sich gegenüber dem rechten Winkel.

2. Aufgabe

$c=50cm$

3. Aufgabe

$c=42,3cm$

M216: Kreis und Kugel

Wie groß ist die Fläche einer Ringstraße, wenn der äußere Ring den Radius 2 km hat, und die Straße 20 m breit ist.
Wie groß sind Volumen und Oberfläche einer Kugel mit Radius 1 m?
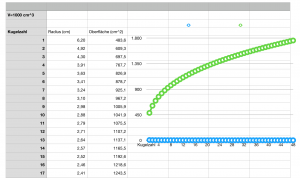
Ein Kaktus teilt sein Volumen von 1 Liter auf eine Kugeln auf. Ein anderer Kaktus teilt das selbe Volumen auf zwei Kugeln auf. Ein weiterer Kaktus teilt dieses Volumen auf drei Kugeln auf. Wie sehr unterscheiden sich die Oberflächen dieser Kakteen?

Lösungen

1. Aufgabe

$F=250.000m^2 \text{(gerundet)}$

2. Aufgabe

$V=4,2m^3$

$O=12,6m^2$

3. Aufgabe

Klick zum Vergrößern

M217: Würfel, Quader, Prisma

Berechnen Sie Oberfläche und Volumen eines Würfels mit Seitenlänge a=3m.
Berechnen Sie die Höhe eines Quaders mit quadratischer Grundfläche. Die Grundfläche ist 10 Quadratmeter, das Volumen ist 40 Kubikmeter.
Eine Stange hat die Grundfläche eines rechtwinkeligen Dreiecks mit Katheten 3 cm und 4 cm. Sie ist ein Prisma mit einer Höhe von 3 Metern. Wie schwer ist sie, wenn sie aus Eisen besteht? Eisen hat eine Dichte von 8 g pro Kubikzentimeter.

Lösungen

1. Aufgabe

$O=54m^2$

$V=27m^3$

2. Aufgabe

$h=4m$

3. Aufgabe

$\text{Grundflaeche} =12cm^2$

$V=3600 cm^3$

$m=28,8 kg$

M218: Zylinder, Kegel

Eine zylindrische Regentonne hat einen Innendurchmesser von 60 cm und eine Höhe von 85cm. Wie viel Liter Wasser (V) fasst sie? Wie hoch (h) stehen 150 Liter Regenwasser in ihr?
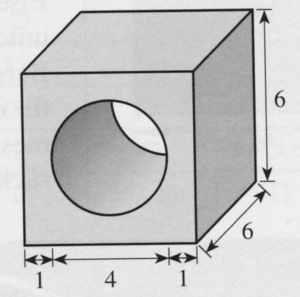
Das abgebildete Werkstück stellt einen Quader dar, in den ein Zylinder eingefräst wurde. (Maße in Zentimeter). Welches Volumen (V) besitzt das Werkstück? Das Werkstück soll komplett mit Farbe bestrichen werden. Wie groß ist die zu bestreichende Fläche (O)?
Klick zum Vergrößern
Angenommen ein Kaktus möchte sein Volumen von 1 Liter in Form eines Kegels aufteilen. Wie hoch wäre dieser Kegel, wenn die Grundfläche den selben Radius hätte als der Kaktus als Kugel?

Lösungen

1. Aufgabe

$V=240l$

$h=53cm$

2. Aufgabe

$V=216cm^3-75cm^3=141cm^3$

$A=141cm^2$

3. Aufgabe

$r=6,2cm$

$h_{Kegel}=25cm$

Grundlagen der Mathematik 2 – Übungsaufgaben

M201: Zahlen den Zahlenmengen zuordnen

Lösungen

M202: Rechengesetze für Potenzen

Lösungen

M203: Potenzen mit rationalen Exponenten (Wurzeln)

Lösungen

M204: Rechnen mit Wurzeln: Zahlen und Terme “in” und “aus” einer Wurzel bringen

Lösungen

M205: Dekadisches Zahlensystem, Gleitkommadarstellung, Abkürzungen

Lösungen

Lösung

M206: Einfache Textbeispiele überschlagsmäßig und genau rechnen

Lösungen

M207: Potenzen in Termen vereinfachen, herausheben und ausmultiplizieren

Lösungen

M208: Binomische Formeln

Lösungen

M209: Formeln umformen

Lösungen

M210: Lineare Gleichungen

Lösungen

M211: Produkt-Null-Satz

Lösungen

M212: Bruchgleichungen

Lösung

M213: Quadratische Gleichungen

Lösungen

M214: Lineare Gleichungssysteme

Lösungen

M215: Lehrsatz des Pythagoras

Lösungen

M216: Kreis und Kugel

Lösungen

M217: Würfel, Quader, Prisma

Lösungen

M218: Zylinder, Kegel

Lösungen

Kommentar absenden Antworten abbrechen