Wörter 1
das Diagramm, der Sand, das Meer, verstehen, zeichnen, die Zeichnung, die Skizze, zunächst, genau, wirklich, das Leben, das Programm, der Computer, das Computerprogramm, die Arbeit, nehmen, abnehmen, zeigen, das Verhältnis, zueinander, sehen, das Beispiel, stehen, bestehen, der Teil, kommen, das Silizium, das Siliziumdioxid

Diagramme gibt’s wie Sand am Meer. Um sie zu verstehen, werden wir einige zeichnen. Zunächst als Skizzen, dann auch genau. Im „wirklichen Leben“ werden uns Computerprogramme diese Arbeit abnehmen.
1. Was ist ein Diagramm?
Ein Diagramm ist eine Zeichnung. Sie zeigt mehrere Zahlen und ihre Verhältnisse zueinander. Wir sehen uns das an einem Beispiel an. Woraus besteht Sand? Aus Siliziumdioxid. SiO2. Zwei Teile Sauerstoff kommen auf einen Teil Silizium.


Straßenverkehr wird oft in Diagrammen dargestellt. Die Zeichen am Boden heißen übrigens Piktogramme. Ein Diagramm ist das, was wir auf Papier oder dem Bildschirm zeichnen.
Wörter 2
das Diagramm, das Piktogramm, die Grafik, zeichnen, die Zeichnung, der Anteil, verständlich, darstellen, viele/mehrere, das Beispiel, sehen, ansehen, zeigen, verschieden, die Art, das Fahrzeug, die Kraft, das Kraftfahrzeug, das Auto, der Personenkraftwagen (Pkw), der Rest, der Motor, das Rad, das Motorrad, das Zweirad, die Last, der Wagen, der Lastkraftwagen (Lkw), die Art, die Statistik, Austria, registrieren, das Vorjahr, die Zulassung, neu, die Neuzulassung
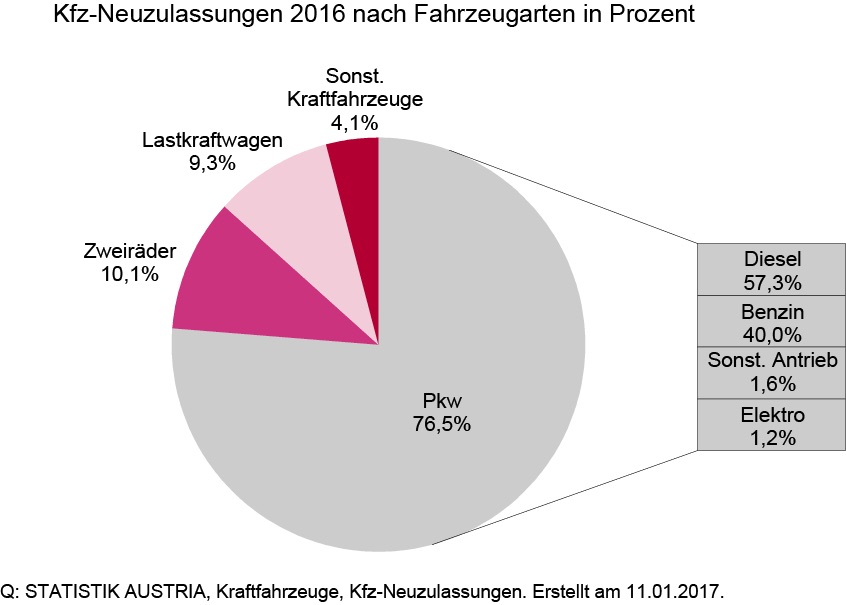
Wir möchte nun in einem Diagramm zeigen, dass es verschiedene Arten von Kraftfahrtzeugen gibt. Die meisten sind Autos (Pkw), und der Rest sind Motorräder (Zweiräder), Lastkraftwagen (Lkw) und sonstige Arten. Die Statistik Austria hat Zahlen, wie viele dieser Arten im vorigen Jahr neu registriert wurden (Neuzulassungen).
Fragen
Wörter 2a
ablesen, verstehen, der Wert, der Durchschnitt, die Division, kennen, nennen, stimmen, wissen, das Verhältnis, ungefähr, der Kreis, schlagen, nachschlagen

Wie viele Pkw wurden 2016 neu zugelassen?
Das können wir aus dem Diagramm nicht ablesen.
Was bedeutet dann Pkw 76,5%?
Von 100 Kraftfahrzeugen die 2016 neu zugelassen wurden, waren 76,5% Pkw.
76 ist verständlich. Es gibt aber keine 0,5 Pkw. Wie soll man das verstehen?
76,5% ist ein Durchschnittswert. Das Prozentzeichen % sagt, dass dieser Wert aus der Division zweier Zahlen entstanden ist. Wir kennen diese Zahlen nicht, sie werden im Diagramm nicht genannt.
Was können wir dann über die Neuzulassungen 2016 sagen?
- Von 100 sind 76,5% Pkw
- Von 1.000 sind 765 Pkw
- Von 10.000 sind 7.650 Pkw
- Von 100.000 sind 76.500 Pkw
- Von 1.000.000 sind 765.000 Pkw
- … und so weiter
Was davon stimmt?
Das wissen wir nicht. Aber im Verhältnis zu den anderen Kraftfahrzeugen sind die meisten neu zugelassene Pkw. Ungefähr 3/4. Das sehen wir im Diagramm.
Warum 3/4?
Auch das sieht man im Diagramm. Der ganze Kreis besteht aus 4 Teilen. Ungefähr 3 Teile sind die Pkw. Das ist der Vorteil eines Diagramms. Wir brauchen uns nicht mit dem genauen Wert 76,5% zu beschäftigen. Wir sehen ganz schnell „drei Viertel“.
Stimmt das wirklich?
Klar. Wenn wir 3 durch 4 dividieren, erhalten wir 0,75. Das sind 75%. Das ist ungefähr 76,5%.
Woher kommt aber jetzt dieses 76,5%?
Jemand hat die Zahl der neu zugelassenen Pkw durch die Zahl aller neu zugelassenen Kraftfahrzeuge dividiert. Wir können das auch hier nachschlagen: Link
Aufgabe
Wörter 3
der Link, finden, heraus, herausfinden, stehen, entstehen, insgesamt, der Verkehr, das Jahr, vorher, das Vorjahr, aktuell, die Daten (Mehrzahl), das Stück, gegenüber, die Stelle, das Komma, das Hundertstel, die Hundertstelstelle
Finden Sie über den Link die Zahlen heraus, aus denen 76,5% entstanden ist.
Lösung
Weitere Fragen
Wörter 4
der Diesel, das Benzin, der Antrieb, sonstig, die Elektrizität, der Elektroantrieb, der Balken, grau, rechts, neben, das Diagramm, der Kreis, das Kreisdiagramm, beziehen, beschreiben, die Art, der Antrieb, die Antriebsart, verwenden, nennen, die Größe, der Sektor, der Kreissektor, ungefähr, gleich, grafisch
Was sagen die grauen Balken rechts neben dem Kreisdiagramm?
- Sie beziehen sich auf die Pkw
- Sie beschreiben, welche Antriebsarten verwendet werden
- Die Prozentanteile werden genannt
Beim Kreisdiagramm können wir aus der Größe der Kreissektoren den ungefähren Anteil erkennen. Die grauen Balken sind gleich breit. Sie stellen die Prozentanteile nicht grafisch dar.
2. Ein Kreisdiagramm selbst machen – Stufe 1
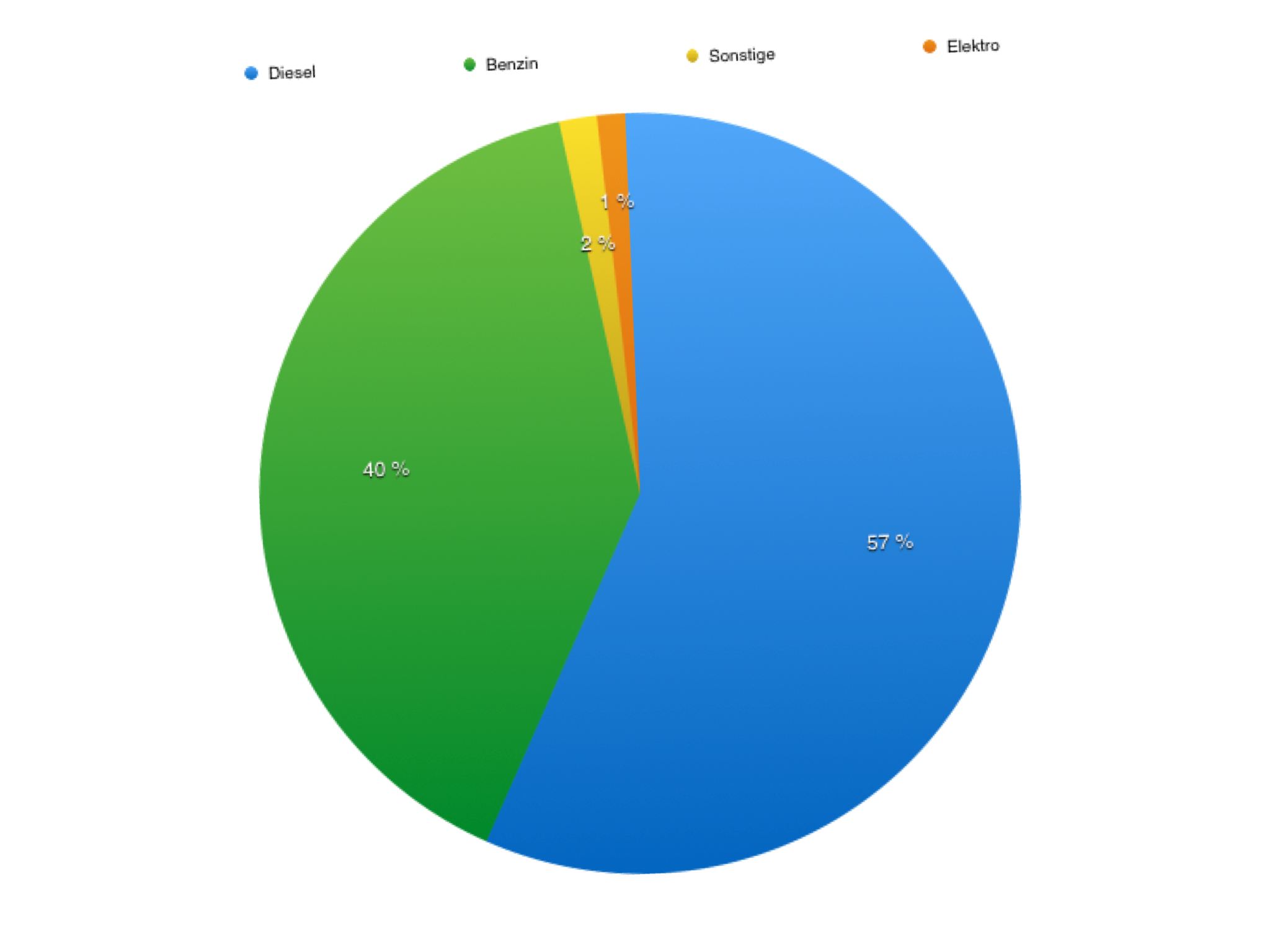
Wir möchten die grauen Balken von vorhin als Kreisdiagramm darstellen. Wir möchten zeigen, womit die Pkw, die 2016 neu zugelassen wurden, angetrieben werden.
Diesel … 57,3%
Benzin … 40,0%
Sonstige Antriebe … 1,6%
Elektro … 1,2%
Wörter 5
der Diesel, das Benzin, der Antrieb, sonstige, die Elektrizität, der Elektroantrieb, vorhin, das Diagramm, der Kreis, das Kreisdiagramm, grau, der Balken, treiben, antreiben, die Methode, schnell, schmutzig, ganz, halb, erhalten, indem, das Viertel, groß, klein, teilen, der Teil, zerteilen, das Lineal, messen, die Messung, der Winkel, der Winkelmesser
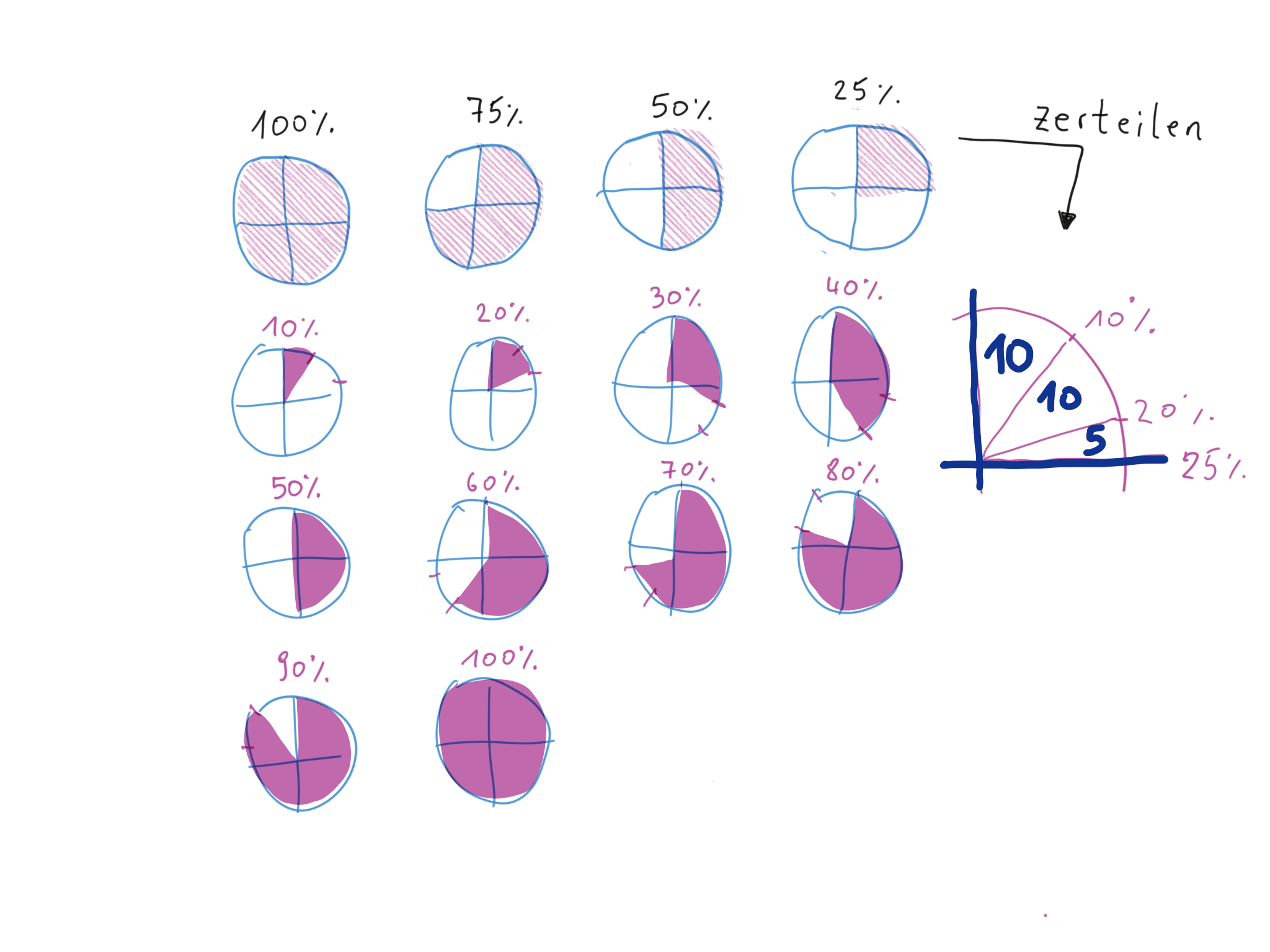
Methode „schnell und schmutzig“
Wir zeichnen ohne Lineal und Winkelmesser. Ein ganzer Kreis: 100%, ein halber Kreis: 50%. 10% erhalten wir, indem wir ein Viertel eines Kreises in zwei große und einen kleinen Teil teilen.
Methode „genau“
Wörter 6
arbeiten, das Grad, der Winkel, das Segment, der Kreis, das Kreissegment, voll, halb, viertel, rund, kommen, herauskommen, zeichnen, selten, der Winkel, der Winkelmesser, der Bleistift, tippen, die Tabelle, die Kalkulation, die Tabellenkalkulation, drücken, erstellen, wissen, die Grundlage, der Fehler, tippen, der Tippfehler
Wir arbeiten mit Grad für den Winkel des Kreissegments.
- 360 Grad … voller Kreis … 100%
- 180 Grad … halber Kreis … 50%
- 90 Grad … Viertelkreis … 25%
- 10% sind 1/10 von 360 Grad, also 36 Grad
- 1% sind 1/100 von 360 Grad, also 3,6 Grad
Wenn 3,6 Grad 1% sind …
- … dann sind 57,3% 3,6*57,3 = rund 206 Grad
- … dann sind 40% 3,6*40 = 144 Grad
- … dann sind 1,6% 3,6*1,6 = rund 6 Grad
- … dann sind 1,2% 3,6*1,2 = rund 4 Grad
Insgesamt sollten 360 Grad herauskommen. Der ganze Kreis. 100%
Diese Diagramme zeichnen wir selten mit Winkelmesser und Bleistift. Wir tippen die Daten in eine Tabellenkalkulation und drücken „Kreisdiagramm erstellen“. Wir sollten aber wissen, wie man das macht. Das gehört zu den Grundlagen. Es hilft uns auch, Tippfehler zu finden, oder andere Fehler.
3. Ein Kreisdiagramm selbst machen – Stufe 2
Im letzten Beispiel waren die Prozentangaben bereits vorhanden. Was aber, wenn wir diese Prozentangaben nicht haben? Dann berechnen wir sie. Wieder ohne Tabellenkalkulation, um die Grundlagen zu lernen.
Wörter 7
selbst, machen, das Beispiel, das letzte Beispiel, rechnen, berechnen, die Grundlage, die Tabelle, die Kalkulation, die Tabellenkalkulation, der Inhalt, der Stoff, der Inhaltsstoff, das Müsli, das Fett, das Kohlenhydrat (neu: das Kohlehydrat), das Eiweiß, der Ballaststoff, das Salz, vernachlässigen, unbestimmt, der Fehler, runden, die Rundung, der Rundungsfehler, kontrollieren, die Kontrolle
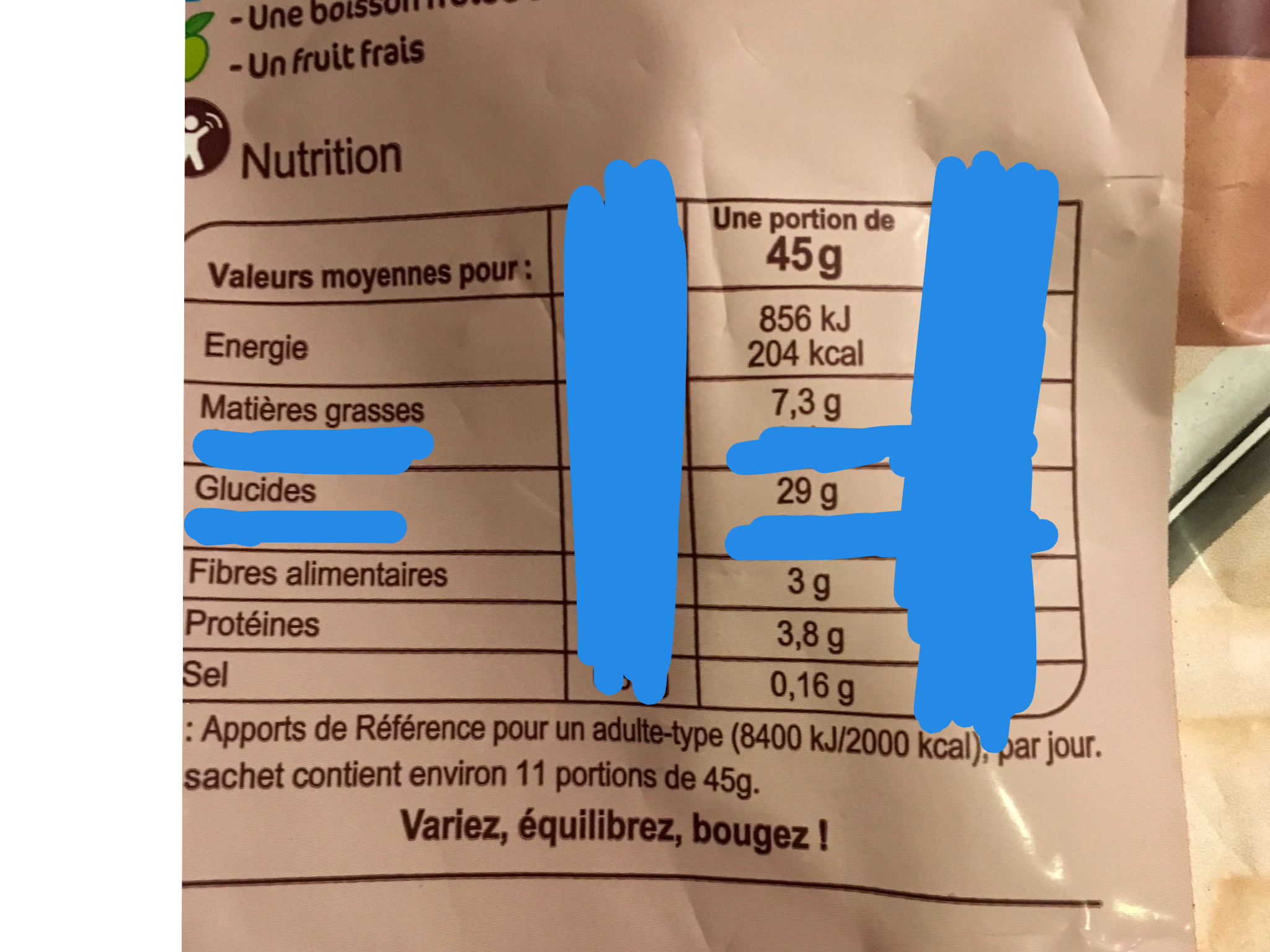
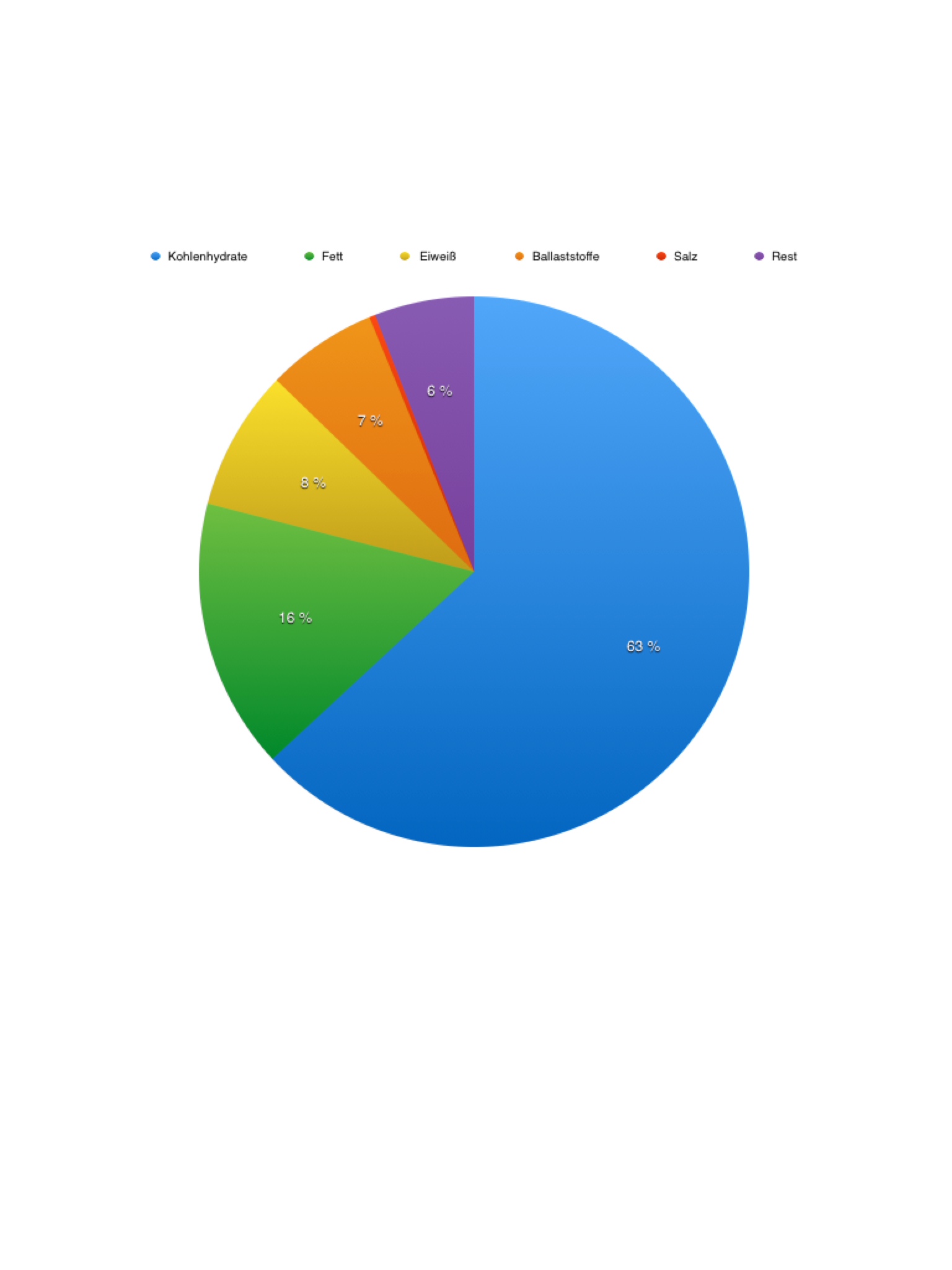
Wir möchten die Inhaltsstoffe des Müslis in einem Kreisdiagramm darstellen. Dazu können wir wieder schnell & schmutzig arbeiten, oder genau.
Schnell & Schmutzig: wir arbeiten in %
100% … 45 g
100% : 45 … 1g = 2,22%
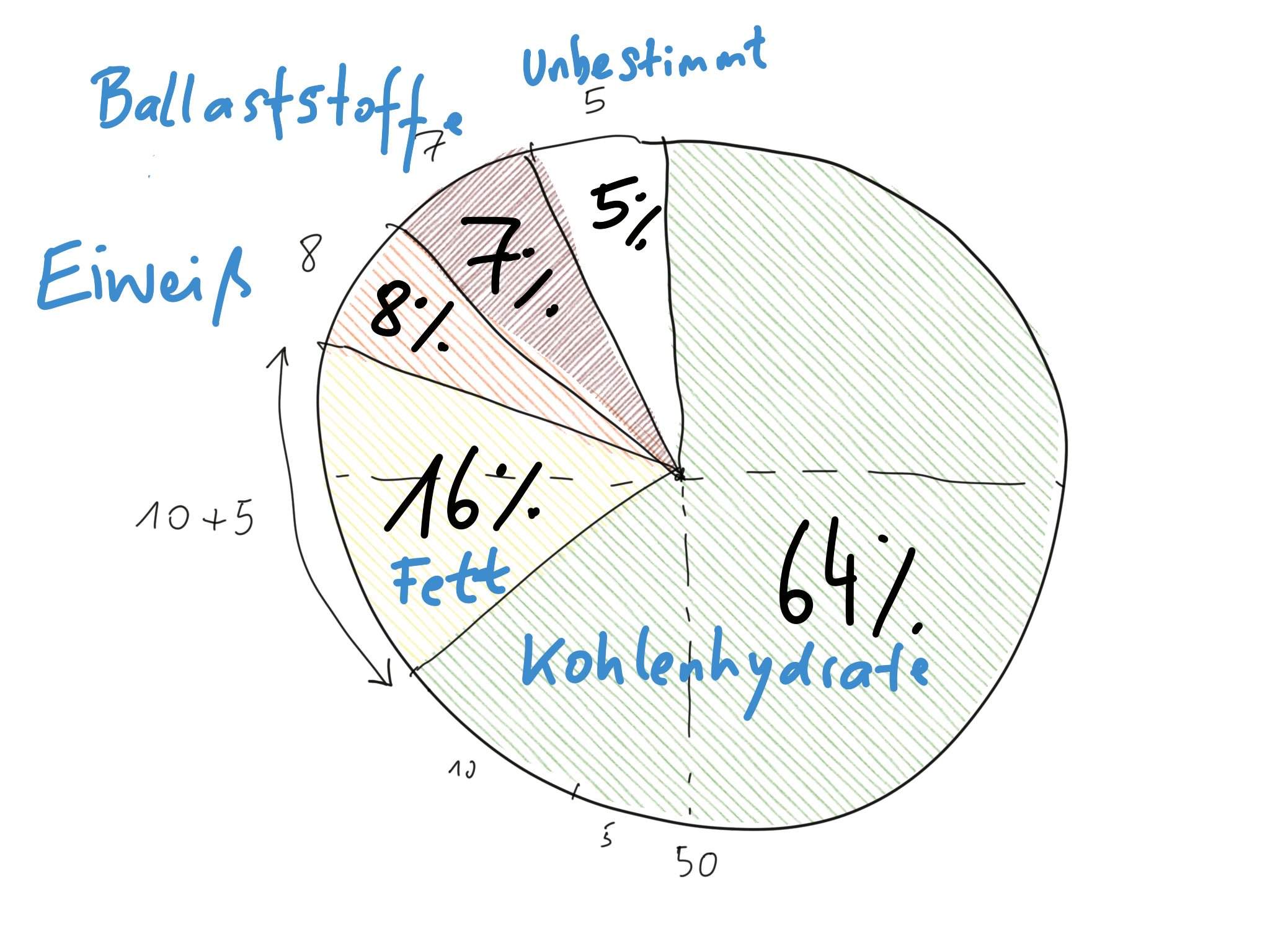
- 7,3 g … 7,3*2,22% = rund 16% … Matières grasses (Fett)
- 29 g … 29*2,22% = rund 64% … Glucides (Kohlenhydrate)
- 3 g … 3*2,22% = rund 7% … Fibres alimentaires (Ballaststoffe)
- 3,8 g … 3,8*2,22 = rund 8% … Protéines (Eiweiß)
- 0,16 g … 0,16*2,22 = rund 0% … Sel (Salz) … vernachlässigbar im Diagramm
Kontrolle: 100% – 16% – 64% – 7% – 8% = 5% unbestimmt /Rundungsfehler
Genau
Bei der genauen Rechnung nehmen wir wieder 360 Grad für das Ganze. 360 Grad sind die gesamte Menge – 45 g. Prozente benötigen wir nicht.
Wörter 8
genau, die Rechnung, nehmen, das Grad, das Ganze, gesamt, die Menge, rund, unbestimmt, der Fehler, der Rundungsfehler, die Kontrolle, üblicherweise, ordnen, die Größe, der Größe nach, der Sektor, manchmal, das Argument, gut, anders, die Reihenfolge
360 Grad … 45 g
360 Grad : 45 … 1 g = rund 8 Grad
- 7,3 g … 7,3*8 Grad = rund 58 Grad … Matières grasses (Fett)
- 29 g … 29*8 Grad = 232 Grad … Glucides (Kohlenhydrate)
- 3 g … 3*8 Grad = 24 g Grad … Fibres alimentaires (Ballaststoffe)
- 3,8 g … 3,8*8 Grad = Rund 30 Grad … Protéines (Eiweiß)
- 0,16 g … 0,16*8 Grad = rund 1 Grad … Sel (Salz) … vernachlässigbar im Diagramm
Kontrolle: 360 – 58 – 232 – 24 – 30 = 16 Grad … Unbestimmt /Rundungsfehler
4. Ein Balkendiagramm erstellen
Es gibt viele Arten von Diagrammen. Wer keine Kreise mag, nimmt Balken.
Wörter 9
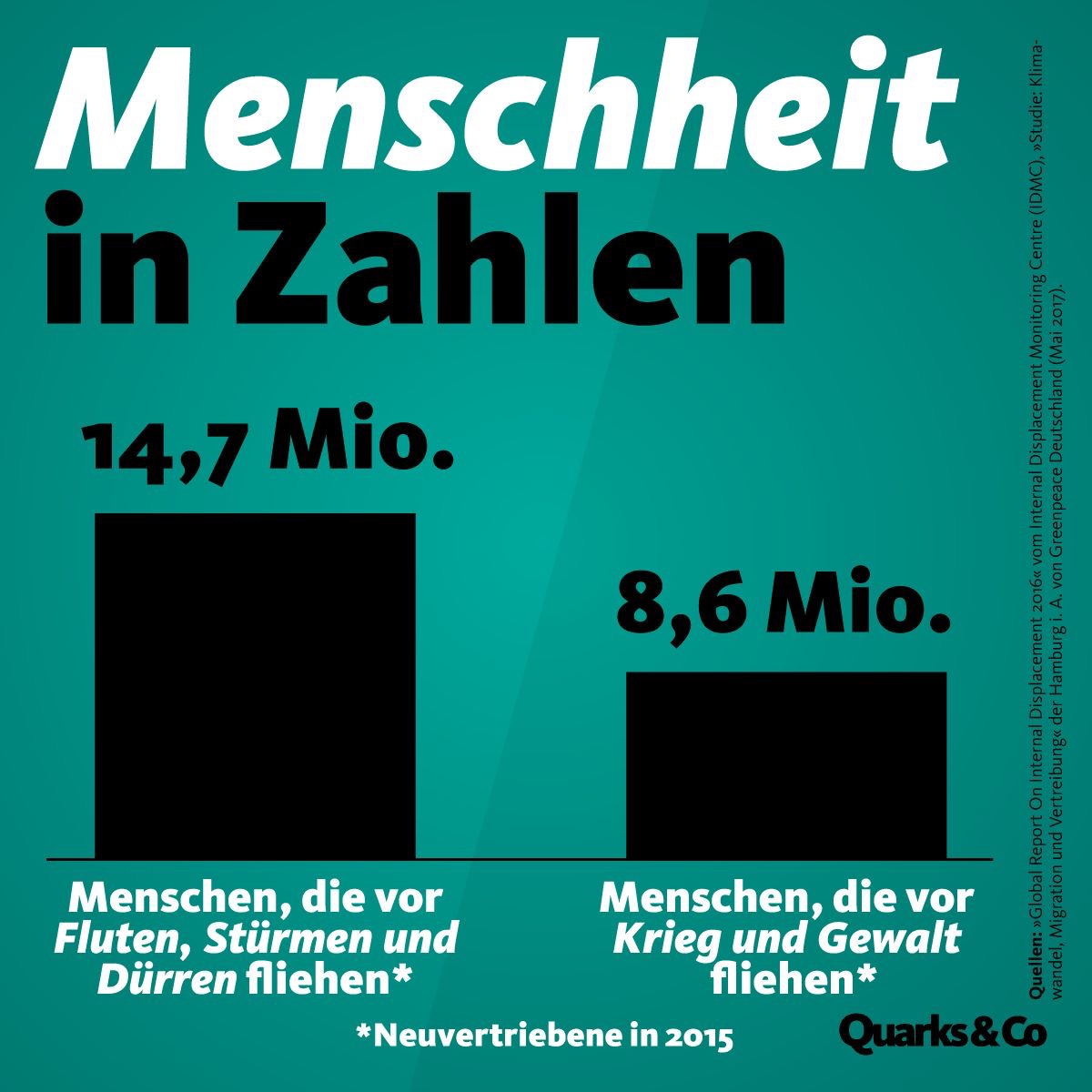
viel, die Art, mögen, nehmen, der Balken, die Menschheit, fliehen, die Flut, der Sturm, die Dürre, der Krieg, die Gewalt, der Vertriebene, neu, der Neuvertriebene, überlegen, die Höhe, Platz, runden, gerundet, die Einheit, der Wert, vertrauen, bald, selbst, gewünscht
Wir überlegen uns die Höhe des größten Balkens. Wie viel Platz haben wir dafür? Sagen wir 3 cm.
- 3 cm sind 14,7 Millionen
- 3 cm : 14,7 = 0,204 cm sind 1 Million
- 0,204 cm * 8,6 sind gerundet 1,8 cm
5. Ein Liniendiagramm erstellen
Es gibt viele Arten von Diagrammen. Oft sind Linien passend, Zahlen und ihre Verhältnisse darzustellen. Liniendiagramme verwenden wir oft, wenn wir den zeitlichen Verlauf zeigen möchten. Sie funktionieren mit Zahlen oder Zahlenverhältnissen (in %).
Wörter 10
die Linie, passen, das Verhältnis, darstellen, das Diagramm, das Liniendiagramm, oft, zeitlich, der Verlauf, zeigen, möchten, funktionieren, das Zahlenverhältnis, der Tag, die Temperatur, hoch/höher/am höchsten, die Tageshöchsttemperatur, Montag, Dienstag, Mittwoch, Donnerstag, Freitag, Samstag, Sonntag, die Woche, die letzte Woche, darstellen, zeichnen, das Grad, Grad Celsius, der Punkt, kariert, das Papier, legen, festlegen, das Kästchen, die Stelle, richtig
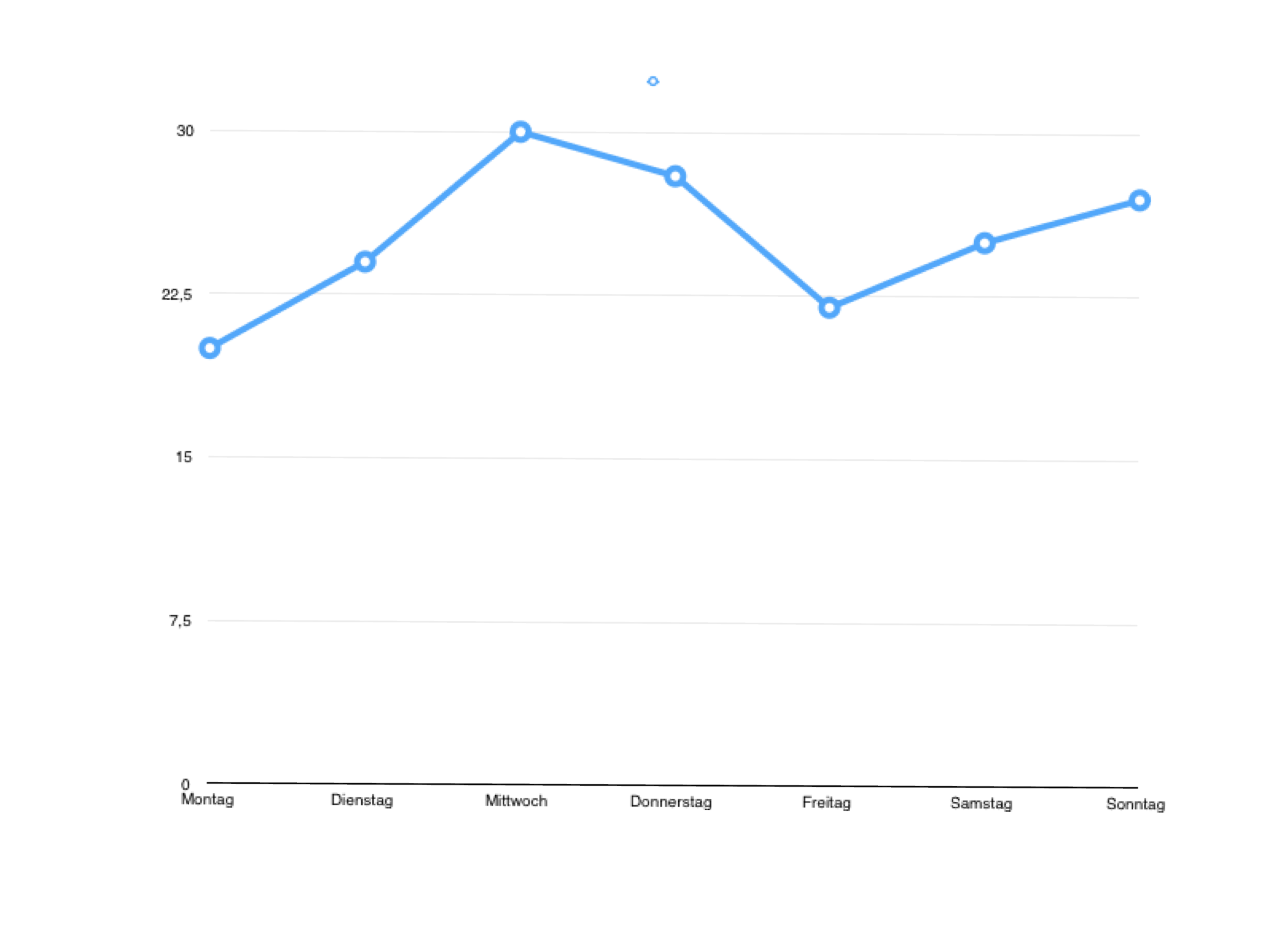
Beispiel
Die Tageshöchsttemperaturen betrugen letzte Woche 20 Grad (Montag), 24 Grad (Dienstag), 30 Grad (Mittwoch), 28 Grad (Donnerstag), 22 Grad (Freitag), 25 Grad (Samstag) und 27 Grad (Sonntag). Wir stellen das in einem Liniendiagramm dar. Wir zeichnen es.
6. Eigene Übungen
Wörter 11
passiv, aktiv, die Zeitung, das Internet, sehen, umsehen, sammeln, das Kreisdiagramm, das Balkendiagramm, das Liniendiagramm, studieren, erklären, jemandem, der Alltag, sammeln, versuchen, zeigen, oft, immer, möglich, sinnvoll, erklären
Passiv
Sehen Sie sich in Zeitungen und im Internet um, und sammeln Sie Kreisdiagramme, Balkendiagramme, Liniendiagramme. Studieren Sie diese Diagramme. Erklären Sie diese Diagramme jemandem.
Aktiv
Sehen Sie sich im Alltag um und sammeln Sie Zahlen, die Sie in Kreisdiagrammen, Balkendiagrammen und Liniendiagrammen selbst darstellen. Versuchen Sie dabei immer auch zu zeigen, wo oder was das Ganze ist (100%). Das ist oft, aber nicht immer möglich oder sinnvoll. Erklären Sie dann auch, warum.
7. Erweiterungen: Excel und Wolfram Alpha
Diagramme sollte jeder einmal mit der Hand gezeichnet haben. Dann aber verwenden wir lieber elektronische Hilfsmittel. Excel/Numbers und Wolfram Alpha, GeoGebra. Versuchen Sie bitte, einige Diagramme elektronisch herzustellen. Es wird Ihnen gelingen. Wenn Sie einmal Fehler machen, erkennen Sie sicher bald, was Sie tun müssen, dass alles richtig funktioniert.
Wörter 12
einmal, die Hand, verwenden, lieber, elektronisch, das Mittel, die Hilfe, das Hilfsmittel, herstellen, gelingen, der Fehler, erkennen, bald, sicher, tun, alles, funktionieren

8. Alles Liebe
Wörter
alles, die Liebe, Alles Liebe (Gruß), schaffen, bis, hierher, die Gratulation, dieses Kapitel, die Wörter, vielleicht, schwierig/schwieriger/am schwierigsten, die Bezeichnung, die Möglichkeit, lernen, kennenlernen, der Balken, der Kreis, die Linie, das Diagramm, schön, der Kurs, der Sommer, der Sommerkurs, dabei sein
Wenn Sie es bis hierher geschafft haben, Gratulation. Bei diesem Kapitel waren vielleicht die Wörter das Schwierigste. Alles hat eine Bezeichnung. In diesem Kapitel hatten Sie eine gute Möglichkeit, diese Bezeichnungen kennenzulernen. Balken, Kreis, und Linie. Das Diagramm.
Schön, dass Sie bei diesem Sommerkurs dabei sind.
Korrekturen: Maria Fatoba
Fehler gefunden? Bitte schicken Sie ein E-Mail an fehler@phyx.at. Vielen Dank!