Physikalische Soiree | Wissen

Autor: Redaktion

  • Eisbilder

  • Der Fahrsteig am Flughafen

    Der Fahrsteig am Flughafen

    Fahrsteige sind wie Rolltreppen, die nicht nach oben führen. Fahrsteige sind wie Gehsteige, die sich bewegen. Fahrsteige sind wie Fließbänder.

    Was ist ihr Zweck? Diskutieren Sie darüber.

    Welche Geschwindigkeiten lassen sich im folgenden Video feststellen? Gemeint sind hier: Relativgeschwindigkeiten. Jemand bewegt sich in Bezug zu jemand anderem.

    https://youtu.be/gIo-zvVYWUc

    Das Video wurde am Flughafen Schipol in Amsterdam gemacht. Hinweis: Fußgänger bewegen sich üblicherweise mit rund 4 km/h und Fahrsteige zwischen 0,45 und 0,75 m/s. Nehmen Sie einen sinnvollen Wert an.

    Was Sie hier lernen: Annahmen treffen, Geschwindigkeiten als Relativbewegungen zu erkennen, Einheiten umrechnen, Bewegungen analysieren, in einem Video Prozesse erfassen und beschreiben, Inertialsysteme erkennen.

    Link (Wikipedia): https://de.wikipedia.org/wiki/Fahrsteig

  • Was ist Wissenschaft?

  • Verhext?

  • Warum klettern Schnecken hier hoch?

  • Bestätigen und widerlegen

    Bestätigen und widerlegen

    Bestätigen und Widerlegen

    Lesen Sie die Aussagen. Geben Sie an, wie Sie die Aussage bestätigen können, und wie Sie die Aussage widerlegen können. Ist beides möglich?

    1. Alle Schafe sind weiß.

    Bestätigen:

    Widerlegen:

    2. Es gibt mindestens ein weißes Schaf.

    Bestätigen:

    Widerlegen:

    3. Es gibt kein schwarzes Schaf.

    Bestätigen:

    Widerlegen:

    4. Höchstens ein Schaf ist schwarz.

    Bestätigen:

    Widerlegen:

    5. Alle Gegenstände fallen nach unten.

    Bestätigen:

    Widerlegen:

  • Was schützt diese Konstruktion?

  • Der Hochwasserdamm

    Der Hochwasserdamm

    Wie hoch soll man einen Hochwasserdamm bauen?

    Wenn ein Fluss anschwillt, weil Regen oder Schneeschmelze große Wassermengen bringen, schützt ein Hochwasserdamm die Menschen und Siedlungen am Ufer. Doch wie hoch muss man ihn bauen, damit er wirklich sicher ist? Die Antwort ist nicht so einfach, wie es auf den ersten Blick scheint.

    Erfahrungen aus der Vergangenheit

    Früher orientierte man sich oft an den höchsten bekannten Hochwasserständen. Man maß den Pegel beim letzten großen Ereignis und baute den Damm ein wenig höher. Das Problem: Hochwasser sind keine regelmäßigen Ereignisse, sie unterscheiden sich in Ausmaß und Häufigkeit. Ein Ereignis, das einmal in hundert Jahren vorkommt, kann auch im nächsten Jahr wieder auftreten. Deshalb reicht es nicht aus, nur die Vergangenheit zu betrachten.

    Statistische Modelle und Wahrscheinlichkeiten

    Heute verwenden Ingenieur*innen statistische Methoden. Sie analysieren jahrzehntelange Messreihen und berechnen, wie hoch ein Wasserstand bei einem sogenannten „HQ100“ ist – einem Hochwasser, das im Durchschnitt alle 100 Jahre auftritt. Daraus ergibt sich ein Bemessungswert für die Höhe des Dammes. Zusätzlich berücksichtigt man einen Sicherheitszuschlag, denn Unsicherheiten in den Daten, Klimawandel und extreme Wetterlagen können zu höheren Wasserständen führen, als die Statistik vermuten lässt.

    Technische und ökologische Grenzen

    Ein Damm kann nicht beliebig hoch gebaut werden. Mit zunehmender Höhe steigen die Baukosten enorm. Außerdem verändert ein hoher Damm die Landschaft, schneidet den Fluss vom Umland ab und kann ökologische Schäden verursachen. Ingenieur*innen müssen also einen Kompromiss finden: genug Sicherheit für Menschen und Infrastruktur, aber auch Rücksicht auf Natur, Landschaftsbild und Kosten.

    Hochwasserschutz als Gesamtkonzept

    Die Höhe eines Dammes ist nur ein Teil der Lösung. Rückhaltebecken, Flutpolder oder die Renaturierung von Auenlandschaften können dazu beitragen, Hochwasserspitzen abzufangen, bevor sie in den Siedlungsraum gelangen. Im Idealfall kombiniert man technischen Hochwasserschutz mit ökologischen Maßnahmen. Dann braucht auch der Damm nicht unendlich hoch zu sein, sondern ist Teil eines durchdachten Gesamtkonzepts.

    Fazit

    Die Frage „Wie hoch soll man einen Hochwasserdamm bauen?“ lässt sich nicht mit einer festen Zahl beantworten. Es ist eine Abwägung zwischen wissenschaftlichen Prognosen, technischen Möglichkeiten und gesellschaftlichen Entscheidungen. Ein Damm soll so hoch sein, dass er vor den bekannten und wahrscheinlichen Gefahren schützt – und so geplant, dass er in Zukunft bei Bedarf noch verstärkt werden kann.

    Hinweis: Dieser Artikel wurde mit CHatGPT5 erstellt

  • Kraftwerk

    Was ist das für ein Kraftwerk? Warum? (Lösung)
  • Prozent – Routine

    Prozent – Routine

    Wenn du mit Prozenten richtig rechnen möchtest, machst du zum Trainieren viele Aufgaben, die alle sehr ähnlich ablaufen. Du wirst die Unterschiede dann bald spüren. Es gibt keine Abkürzung – du musst durch alle ruhig durch. Dann bist du Prozentprofi.

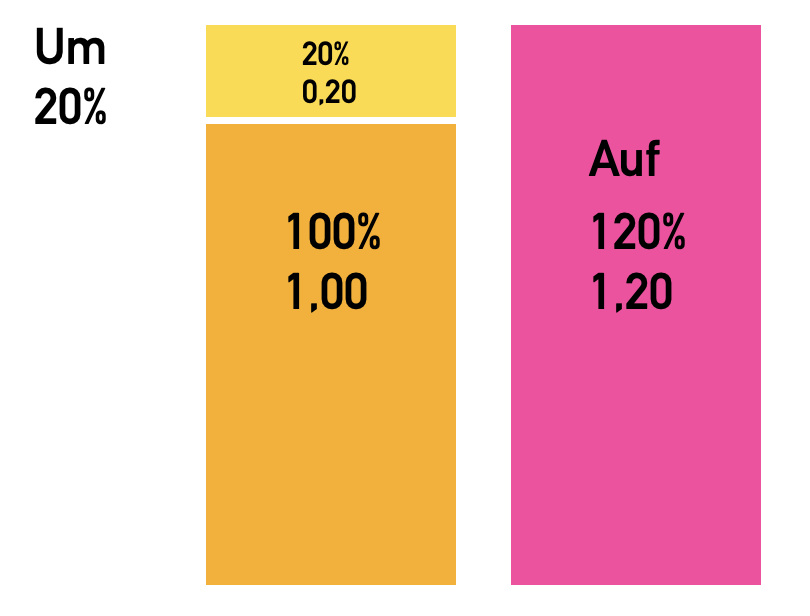
    Um oder auf? Das Prozentrechnen ist ein sprachliches Problem. Wir wollen zuerst den Unterschied zwischen „um“ und „auf“ verstehen.

    Wörter:
    weniger werden = reduziert werden = verkleinert werden = schrumpfen
    mehr werden = erhöht werden = vergrößert werden = ausdehnen

    1. Auf wie viel Prozent ist es gewachsen?
    2. Um wie viel Prozent ist es gewachsen?
    3. Auf wie viel Prozent ist es reduziert worden?
    4. Um wie viel Prozent ist es reduziert worden?

      Du wirst lernen, „auf“ von „um“ zu unterscheiden.
    5. Es ist um einige Prozent gewachsen. Wie viel ist es jetzt?
    6. Es ist auf eine bestimmte Prozentzahl gewachsen. Wie viel ist es jetzt?
    7. Es ist um einige Prozent reduziert geworden. Wie viel ist es jetzt?
    8. Es ist auf eine bestimmte Prozentzahl reduziert worden. Wie viel ist es jetzt?

      Du wirst lernen, „auf“ von „um“ zu unterscheiden.
    9. Es ist um einen bestimmten Prozentwert gewachsen. Wie viel war es vorher?
    10. Es ist auf einen bestimmte Prozentwert gewaschen. Wie viel war es vorher?
    11. Es ist um einen bestimmten Prozentwert reduziert worden. Wie viel war es vorher?
    12. Es ist auf einen bestimmten Prozentwert reduziert worden. Wie viel war es vorher?

      Du wirst lernen, „auf“ von „um“ zu unterscheiden.

    Prozentrechnen bedeutet, die Worte „auf“ von „um“ zu unterscheiden.

    Wenn etwas auf 90% reduziert wurde, ist es um 10% reduziert worden.
    Wenn etwas auf 120% vergrößert wurde, ist es um 20% vergrößert worden.

    weniger werden = reduziert werden = verkleinert werden = schrumpfen
    mehr werden = erhöht werden = vergrößert werden = ausdehnen

    1. Mehr Einkommen! Vorher: 80€, nachher 100€. Auf wie viel Prozent ist es gewachsen?
    2. Mehr Einkommen! Vorher: 300€, nachher 410€. Um wie viel Prozent ist es gewachsen?
    3. Weniger Einkommen! Vorher 150€, nachher 120€. Auf wie viel Prozent ist es reduziert worden?
    4. Weniger Einkommen! Vorher 1000€, nachher 900€. Um wie viel Prozent ist es reduziert worden?
    5. Mehr Gewicht. Vorher 20 kg. Es ist um 10% gewachsen. Wie viel ist es jetzt?
    6. Mehr Gewicht. Vorher 90 kg. Es ist auf 110% gewachsen. Wie viel ist es jetzt?
    7. Weniger Gewicht. Vorher 40 kg. Es ist um 25% reduziert geworden. Wie viel ist es jetzt?
    8. Weniger Gewicht. Vorher 200 kg. Es ist auf 75% reduziert worden. Wie viel ist es jetzt?
    9. Die Geschwindigkeit ist jetzt 50 km/h. Sie ist um 12 Prozent gewachsen. Wie viel war sie vorher?
    10. Die Geschwindigkeit ist jetzt 100 km/h. Sie ist auf 105% gewachsen. Wie viel war sie vorher?
    11. Die Geschwindigkeit ist jetzt 150 km/h. Sie ist um 10% reduziert worden. Wie viel war sie vorher?
    12. Die Geschwindigkeit ist jetzt 90 km/h. Sie ist auf 85% reduziert worden. Wie viel war sie vorher?

    Um oder auf? Wenn uns das klar ist, wird Prozentrechnen einfacher.

    Um oder auf? Vorher 100%. Nachher 120%. Um 20% auf 120%
    Um oder auf? Vorher 90%. Nachher 100%. Um 10% auf 100%

    Lösung

    1. Mehr Einkommen! Vorher: 80€, nachher 100€. Auf wie viel Prozent ist es gewachsen?
      80•x=100 (wir bringen 80 auf die andere Seite durch Division)
      x=100/80=1,25 (das bedeutet 125%)
      Das Einkommen ist auf 125% gewachsen. („Auf„: So viele Prozent sind es jetzt zusammen)
    2. Mehr Einkommen! Vorher: 300€, nachher 410€. Um wie viel Prozent ist es gewachsen?
      300•x=410 (wir bringen 300 auf die andere Seite durch Division)
      x= 410/300=1,37 (gerundet, das bedeutet 137%)
      Das Einkommen ist um 37% gewachsen. („Um„: Das was es von 100% mehr wurde)
    3. Weniger Einkommen! Vorher 150€, nachher 120€. Auf wie viel Prozent ist es reduziert worden?
      150•x=120
      x=120/150=0,80
      Das Einkommen ist auf 80% reduziert worden.
    4. Weniger Einkommen! Vorher 1000€, nachher 900€. Um wie viel Prozent ist es reduziert worden?
      1000•x=900
      x=900/1000=0,90
      Das Einkommen ist um 10% reduziert worden. („Um„: Der Unterschied zu 100%)
    5. Mehr Gewicht. Vorher 20 kg. Es ist um 10% gewachsen. Wie viel ist es jetzt?
      20•1,10=22 kg. (Es sind nun 110%, daher wird mit 1,10 multipliziert)

      Vergößern bedeutet: Mit einem Wert größer als 1 zu multiplizieren.
    6. Mehr Gewicht. Vorher 90 kg. Es ist auf 110% gewachsen. Wie viel ist es jetzt?
      90•1,1=99 kg
    7. Weniger Gewicht. Vorher 40 kg. Es ist um 25% reduziert geworden. Wie viel ist es jetzt?
      40•0,75=30kg (Es hat nun 75%, daher wird mit 0,75 multipliziert)

      Verkleinern bedeutet: Mit einem Wert zwischen 0 und 1 zu multiplizieren.
    8. Weniger Gewicht. Vorher 200 kg. Es ist auf 75% reduziert worden. Wie viel ist es jetzt?
      200•0,75=150kg
    9. Die Geschwindigkeit ist jetzt 50 km/h. Sie ist um 12 Prozent gewachsen. Wie viel war sie vorher?
      x•1,12=50 (Wir bringen 1,12 durch Division auf die andere Seite)
      x=50/1,12 = rund 44,6 km/h
    10. Die Geschwindigkeit ist jetzt 100 km/h. Sie ist auf 105% gewachsen. Wie viel war sie vorher?
      x•1,05=100
      x= 100/1,05 = rund 95,2 km/h
    11. Die Geschwindigkeit ist jetzt 150 km/h. Sie ist um 10% reduziert worden. Wie viel war sie vorher?
      x•0,9=150
      x= 150/0,9 = rund 166,7 km/h
    12. Die Geschwindigkeit ist jetzt 90 km/h. Sie ist auf 85% reduziert worden. Wie viel war sie vorher?
      x•0,85=90
      x=90/0,85 = rund 105,9 km/h

    Das Rechnen mit Prozenten funktioniert am besten, wenn du dir die Situation vorstellst. In Bildern.

    Deine Aufgabe: Erstelle selbst neue Aufgaben 1 bis 12. Dann kannst du es wirklich.