
Drachen werden aus Flächen zusammengesetzt.
Wir sagen im Alltag oft “Fläche”. In der Mathematik sagen wir meist “Flächeninhalt”.
1. Grundübungen
Wörter 1
der Teppich, die Form, das rechtwinkelige Dreieck, kurz/kürzer/am kürzesten, lang/länger/am längsten, der Umfang, die Fläche, der Flächeninhalt, das Rechteck, das Quadrat, der Tisch, das Bild, die Figur, stellen, darstellen, geben, angeben, die Variable
Ein Teppich hat die Form eines rechtwinkeligen Dreiecks. Die beiden kürzeren Seiten sind 3 m und 4 m lang. Die längere Seite ist 5 m lang. Wie groß ist der Umfang des Teppichs? Wie groß ist der Flächeninhalt des Teppichs?
Lösung
Ein Tisch hat die Form eines Rechtecks. Die Seiten sind 2 m und 1 m lang. Wie groß ist der Umfang des Tisches? Wie groß ist der Flächeninhalt des Tisches?
Lösung
Ein Bild hat die Form eines Quadrates. Die Seiten sind 40 cm lang. Wie groß ist der Umfang des Bildes? Wie groß ist der Flächeninhalt des Bildes?
Lösung
Ein Rechteck hat einen Flächeninhalt von 30 cm², eine Seite ist 6 cm lang. Wie lang ist die zweite Seite? Wie groß ist der Umfang?
Lösung
Von einem Dreieck kennt man die Seite a = 6 cm und den Flächeninhalt A = 24 cm².
Wie lang ist die Höhe auf die Seite a?
Lösung
Stellen Sie den Flächeninhalt der Figur mit Hilfe der angegebenen Variablen dar.
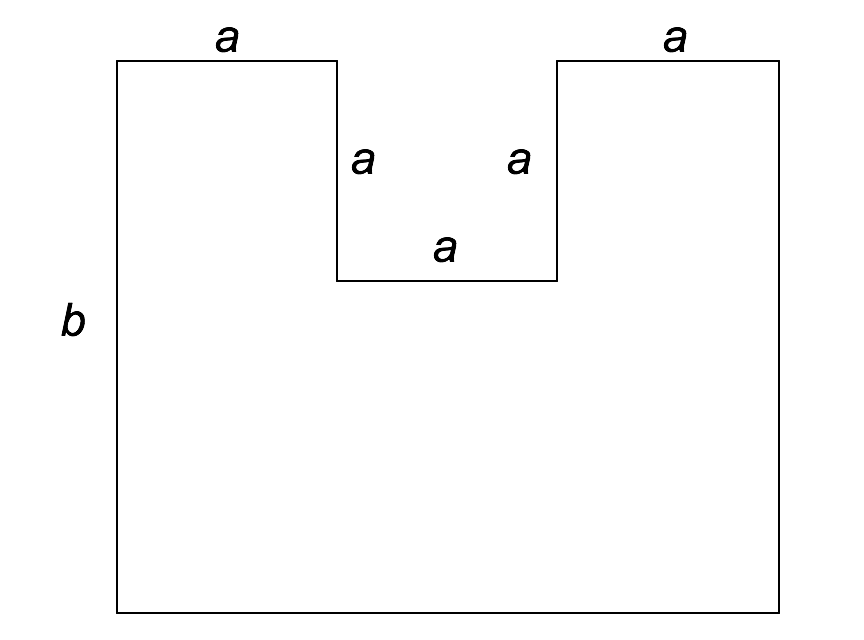
Lösung
2. Weitere Übungen
Wörter 2
das Parallelogramm, die Höhe, das Trapez, das Deltoid, die Diagonale, die Seite, die Raute

Die Tragfläche dieses Drachens besteht aus zwei rechtwinkeligen Dreiecken.
Berechnen Sie bitte den Flächeninhalt eines Parallelogramms. Die Seite a ist 20 cm. Die Höhe auf die Seite a ist 10 cm.
Lösung
Berechnen Sie bitte die Seitenlänge a eines Parallelogramms, von dem der Flächeninhalt und die Höhe auf die Seite a bekannt sind: F = 200 cm², Höhe auf die Seite a = 20 cm.
Lösung
Berechnen Sie bitte den Flächeninhalt eines Trapezes. Die Seite a ist 30 cm. Die Höhe auf die Seite a ist 5 cm und die Seite c ist 8 cm.
Lösung
Berechnen Sie bitte die Höhe h eines Trapezes, von dem der Flächeninhalt und die Seiten a und c bekannt sind: F = 200 cm², Seite a = 20 cm, Seite c = 5 cm.
Lösung
Berechnen Sie bitte den Flächeninhalt eines Deltoids. Die Diagonale e ist 20 cm und die Diagonale f ist 40 cm.
Lösung
Berechnen Sie bitte die Diagonale f eines Trapezes, von dem der Flächeninhalt und die Diagonale e bekannt sind: F = 500 cm², Diagonale e = 20 cm.
Lösung
3. Ausblick
Wir haben in diesem Kurs viele mathematische Methoden kennengelernt. Viel Freude beim Ausprobieren. Keine Angst vor Fehlern – die sehen wir uns im Kapitel 20 noch genauer an. Sie sind wichtig, weil sie uns beim Lernen helfen.
Korrekturen: Maria Fatoba
Fehler gefunden? Bitte schicken Sie ein E-Mail an fehler@phyx.at. Vielen Dank!



