13. Gleichungen lösen | Physikalische Soiree

Sie können lineare Gleichungen umformen, bis die Lösung sichtbar ist.

Wörter 1

gleich, die Gleichung, lösen, die Lösung, die Seite, verschieden, sehen, aussehen, verändern, lesen, ablesen, schreiben, die Klammer, schwingen, die Menge, die Lösungsmenge, erwarten, verstecken, spielen, das Versteckspielen, suchen, schön, schauen, anschauen, lernen, formen, umformen (=verändern), die Äquivalenz (Gleichwertigkeit)

Versteckspiel mit Variablen: Wenn sich eine Variable in einer Gleichung versteckt, dann können wir sie suchen. Wie sieht sie aus? Was wird uns hier erwarten? Bei linearen Gleichungen ist das besonders schön zu lernen. Das schauen wir uns in diesem Kapitel an.

1. Eine Gleichung lösen

Eine Gleichung besteht aus zwei Seiten, die gleich sind. Auch wenn sie verschieden aussehen.

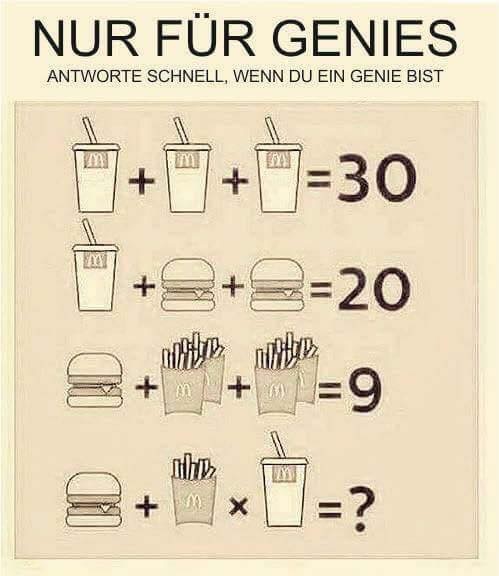
Diese Aufgabe kennen Sie vielleicht aus dem Internet.
Was ist die Lösung? (Quelle: unbekannt)

Lösung

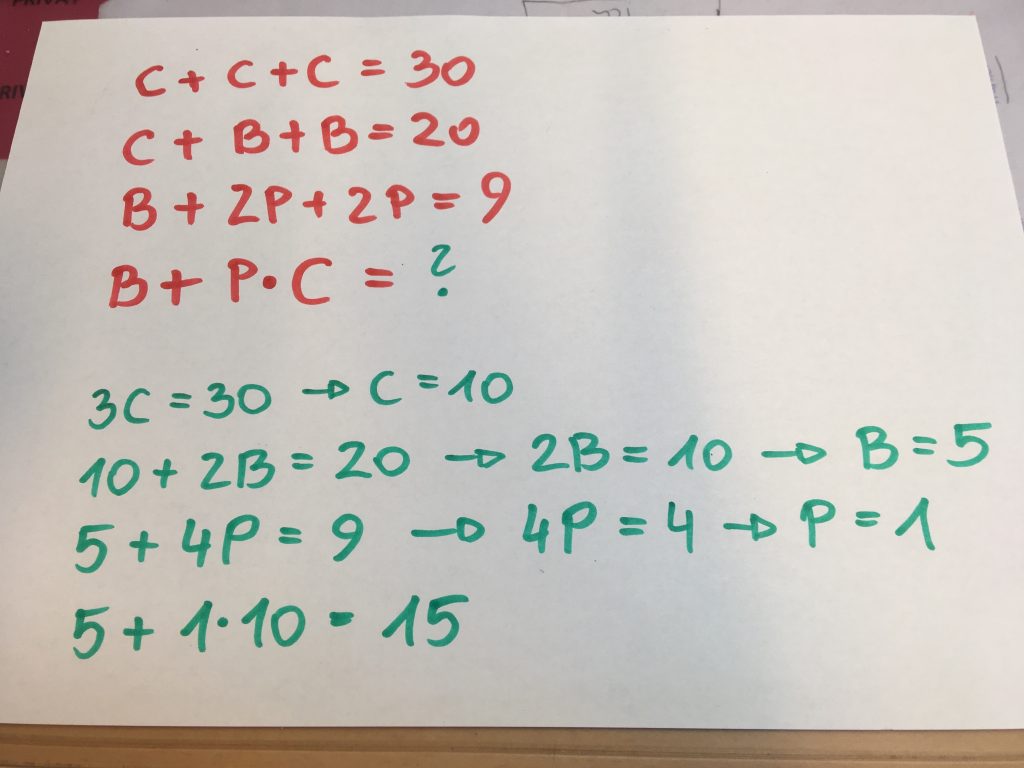
Getränk: 10, Burger: 5, Pommes: 1, Burger + Pommes * Getränk = 15

Beispiel

$\begin {aligned} 2x+4&=10\\ \text {linke Seite}&=\text {rechte Seite}\\ \\ 2x+4&=10 \; \; \longrightarrow \text {auf beiden Seiten}-4\\ 2x&=6 \quad \longrightarrow \text {auf beiden Seiten}:2\\ x&=3 \quad \longrightarrow \text {das ist die L}\ddot o \text{sung}\\ \end {aligned}$

Wir verändern die Gleichung, bis sie so aussieht, dass wir die Lösung leicht ablesen können. Ziel dieser Veränderungen ist, dass x alleine auf der linken Seite steht. Wir machen dazu immer das Gegenteil von dem, was stört. Auf beiden Seiten. Solche Veränderungen werden “Äquivalenzumformungen” genannt. Die gefundene Lösung ist für jede der entstehenden Gleichungen richtig.

Wir schreiben die Lösung zwischen geschwungene Klammern und nennen das die Lösungsmenge L.

$\text {L}=\{ 3 \}$

Übungen

Lösen Sie bitte die folgenden Gleichungen.

$2x+6=10$

Lösung

$\text {L}=\{ 2 \}$

$2x+8=10$

Lösung

$\text {L}=\{ 1 \}$

$2x+10=10$

Lösung

$\text {L}=\{ 0 \}$

$2x+12=10$

Lösung

$\text {L}=\{ -1 \}$

$2x+14=10$

Lösung

$\text {L}=\{ -2 \}$

$2x+16=10$

Lösung

$\text {L}=\{ -3 \}$

$-2x+6=10$

Lösung

$\text {L}=\{ -2 \}$

$2x-6=10$

Lösung

$\text {L}=\{ 8 \}$

$2x+6=-10$

Lösung

$\text {L}=\{ -8 \}$

$-2x+6=-10$

Lösung

$\text {L}=\{ 8 \}$

2. Lineare Gleichungen

Wörter 2

die Gleichung, die Variable, einfach, kompliziert, sogar, der Wert, annehmen, stimmen, linear, quadratisch, der Grad, die Grundlage, eigentlich, beschäftigen, die Probe, setzen, einsetzen, machen

Eine Gleichung hat eine oder mehrere Variablen. Sie kann einfach und kompliziert sein. Sie kann keine, eine oder sogar mehrere Lösungen haben. Eine Lösung ist eine Zahl. Wenn die Variable den Wert dieser Zahl annimmt, dann stimmt die Gleichung.

$5x+1=16 \quad \text{Lineare Gleichung, L=\{3\}}$
$x^2+2x-3=0 \quad \text{Quadratische Gleichung, L=\{-3,1\}}$
$x^3-2x^2-13x-10=0 \quad \text{Gleichung 3. Grades, L=\{-2,-1,5\}}$
$\text{Und so weiter.}$
Wir möchten uns in diesen Grundlagen nur mit der Lösung linearer Gleichungen beschäftigen. Wie wissen wir eigentlich, ob unsere Lösung stimmt? Das zeigt die Probe.

3. Die Probe

$\begin {aligned} 3x-8&=13\\ 3x&=21\\ x&=7 \quad \quad \text{L=\{7\}} \end {aligned}$

Für die Probe setzen wir 7 in die Gleichung ein.

$\begin {aligned} 3 \cdot 7-8&=13\\ 21-7&=13\\ 13&=13 \quad \quad \text{Das stimmt.} \end {aligned}$

7 ist wirklich eine Lösung. Wir haben die Probe gemacht.

Übungen

Machen Sie die Probe in den obigen Übungen.

4. Ausblick

Wir werden uns immer wieder mit linearen Gleichungen beschäftigen. Im nächsten Kapitel werden wir sehen, was sie mit dem Alltag zu tun haben. In weiteren Mathematikkursen werden wir sehen, dass wir diese Gleichungen auch “zeichnen” können. Für den Anfang aber reicht das, was wir hier in diesem Kapitel gemacht haben. Schön, dass Sie dabei sind.

Korrekturen: Maria Fatoba

Fehler gefunden? Bitte schicken Sie ein E-Mail an fehler@phyx.at. Vielen Dank!