Kapitel 05: Primzahlen


 
Wer Primzahlen kennt, kann natürliche Zahlen in ihre „Bestandteile“ zerlegen – die Primfaktoren.

Wörter 1

die Zahl, die Primzahl, kennen, natürlich, natürliche Zahl, der Bestandteil, zerlegen, der Faktor, der Primfaktor


 

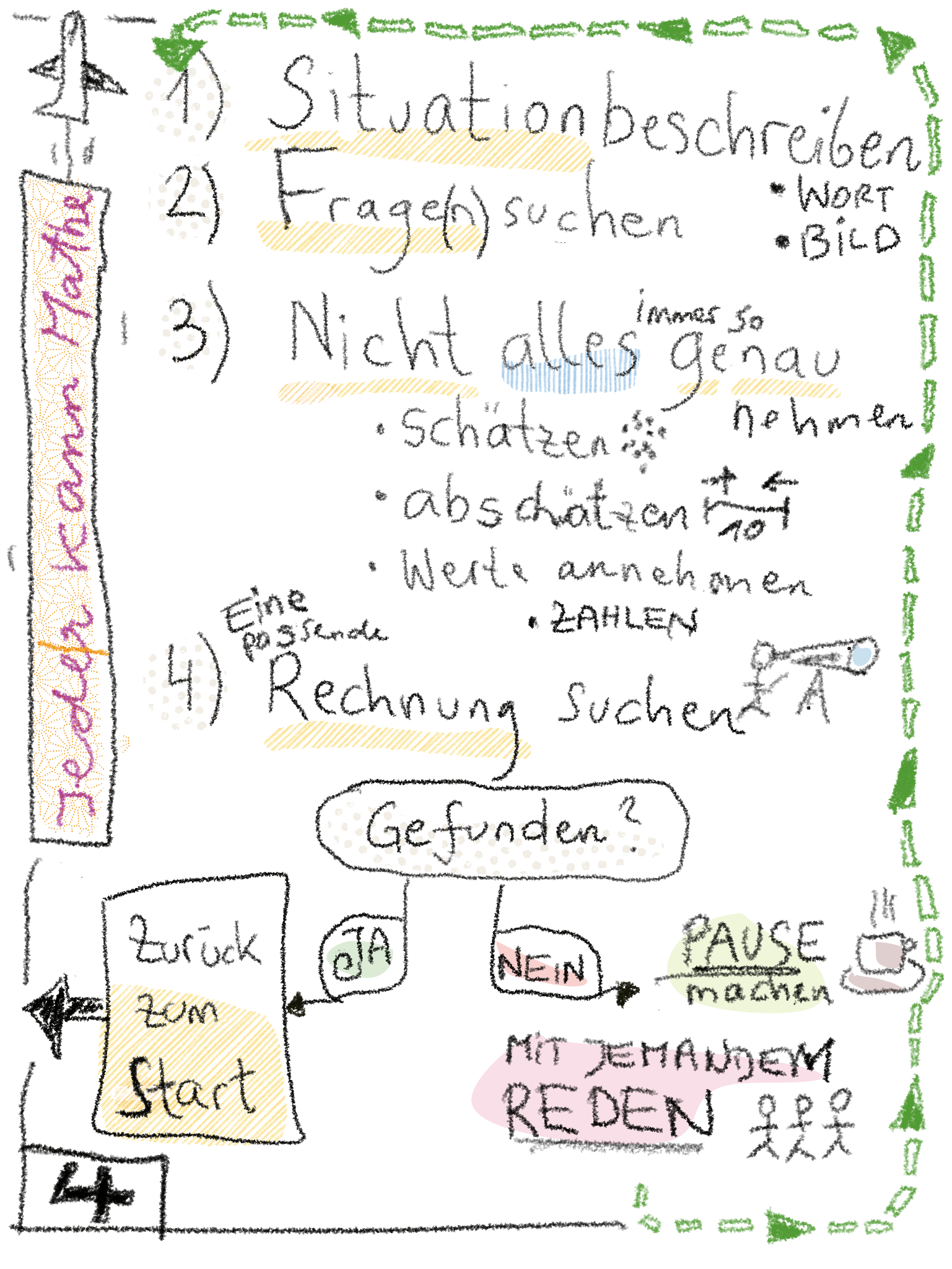
1. Gerecht teilen

Wenn wir etwas gerecht teilen, bekommt jeder gleich viel. Es bleibt kein Rest.

Wörter 1A

gerecht, teilen, der Teil, jeder, gleich, viel, der Rest, der Apfel im Schlafrock (Speise), die Speise, die Möglichkeit, das Stück, die Person, erhalten, die Menge, der Teiler, die Teilermenge, der Markt, das Dutzend


 

Beispiel: „Apfel im Schlafrock“

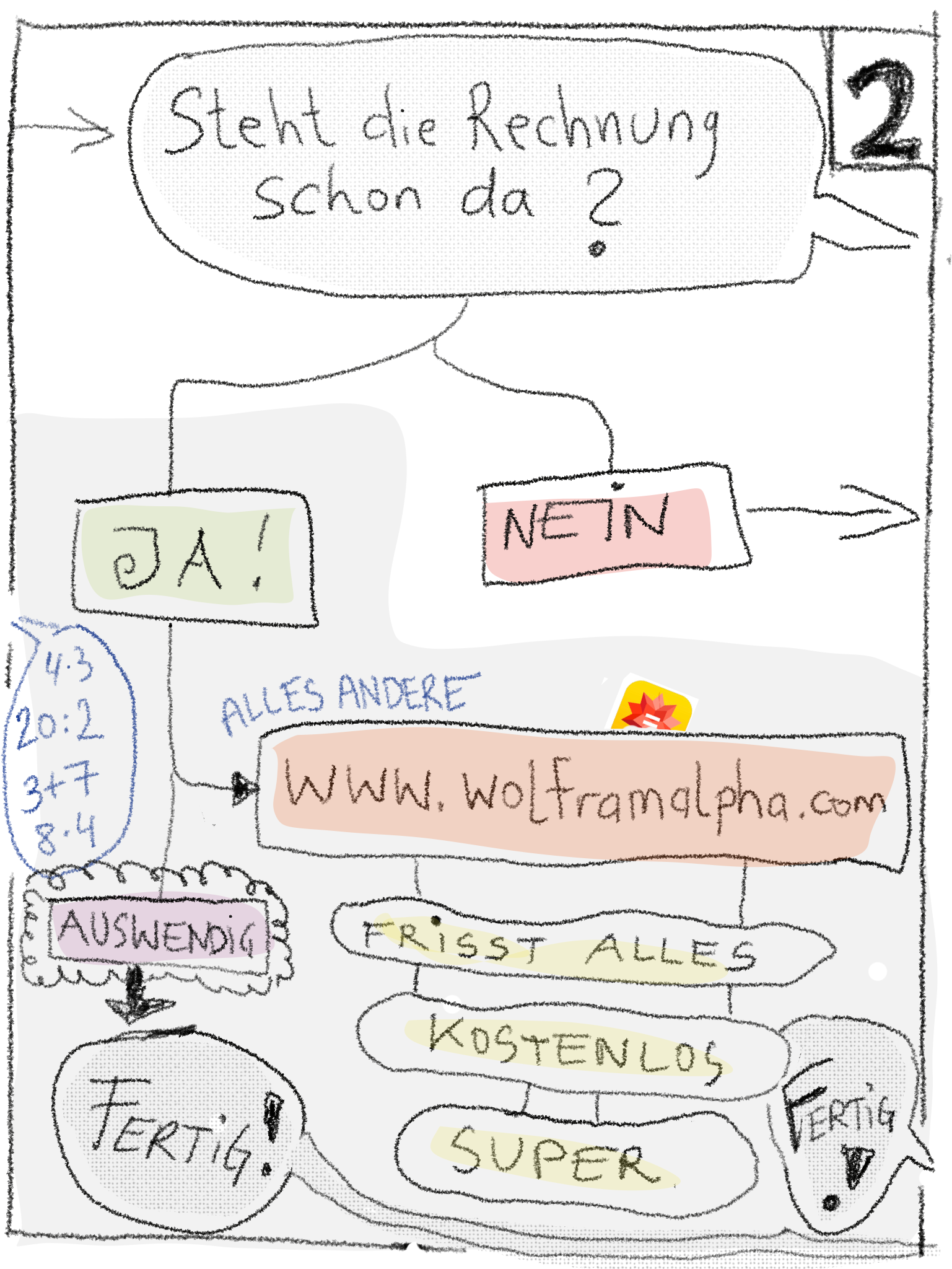
Wie viele Möglichkeiten gibt es, diese Speise ohne Rest zu teilen?
 

Lösung

Es sind 7 Stück.

  • 1 Person erhält 7 Stück
  • 7 Personen erhalten 1 Stück
  • Es gibt keine weiteren Möglichkeiten.

7 kann durch 1 und 7 ohne Rest geteilt werden.

Die Teilermenge von 7 ist 1 und 7.

T_{7}=\{1,7\}
 

Wir nennen 1 und 7 „Teiler“. Sie bilden zusammen die Teilermenge T_{7}

 

Übungen

Ein Dutzend Eier

Wie viele Möglichkeiten gibt es, diese Eier ohne Rest zu teilen?

Lösung

Es sind 12 Stück.

  • 1 Person erhält 12 Stück
  • 2 Personen erhalten 6 Stück
  • 3 Personen erhalten 4 Stück
  • 4 Personen erhalten 3 Stück
  • 6 Personen erhalten 2 Stück
  • 12 Personen erhalten 1 Stück
  • Das sind sehr viele Möglichkeiten.

12 kann durch 1, 2, 3, 4, 6 und 12 ohne Rest geteilt werden.

Die Teilermenge von 12 ist 1, 2, 3, 4, 6 und 12.

T_{12}=\{1, 2, 3, 4, 6,12\}

12 Stück werden auch 1 Dutzend genannt. Besonders am Markt wird dieses Dutzend oft verwendet. Weil man diese Zahl auf so viele verschiedenen Arten teilen kann.

 

Acht Äpfel im Schlafrock

Wie viele Möglichkeiten gibt es, diese Speise ohne Rest zu teilen?

Lösung

Es sind 8 Stück

  • 1 Person erhält 8 Stück
  • 2 Personen erhalten 4 Stück
  • 4 Personen erhalten 2 Stück
  • 8 Personen erhalten 1 Stück

8 kann durch 1, 2, 4, und 8 ohne Rest geteilt werden.

Die Teilermenge von 8 ist 1, 2, 3, 4, und 8.

T_{8}=\{1, 2, 3, 4, 8\}


 

Teilermenge bestimmen

Bestimmen Sie bitte die Teilermengen der Zahlen 16, 20, 36, 100 und 125

Lösung

T_{16}=\{1, 2, 4, 8, 16\}

T_{20}=\{1, 2, 4, 5, 10, 20\}

T_{36}=\{1, 2, 3, 4, 6, 9, 12, 18, 36\}

T_{100}=\{1, 2, 4, 5, 10, 20, 50, 100\}

T_{125}=\{1, 2, 3, 5, 25, 125\}

Bestimmen Sie bitte die Teilermengen der Zahlen 2, 13, 23, 29 und 37

Lösung

T_{2}=\{1, 2\}

T_{13}=\{1, 13\}

T_{23}=\{1, 23\}

T_{29}=\{1, 29\}

T_{37}=\{1, 37\}

2. Primzahlen

Es gibt Zahlen, die eine ganz kleine Teilermenge haben. Nur 1 ist ein Teiler dieser Zahl, und die Zahl selbst. Wir nennen diese Zahlen Primzahlen.

Wörter 2

die Menge, der Teiler, die Teilermenge, nur, selbst, nennen, die Primzahl, auswendig, können, unendlich, das Sieb, finden, groß, lange, dauern

Primzahlen sind natürliche Zahlen.

\mathbb{P}=\{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...\}

Es wäre gut, wenn Sie die Primzahlen bis 20 auswendig können. Das werden Sie oft brauchen. Es gibt unendlich viele Primzahlen. Mit dem „Sieb des Eratosthenes“ können Sie alle finden. Für die großen Primzahlen kann das aber lange dauern.

Aufgabe

Sehen Sie sich dieses animierte GIF an. Es zeigt Ihnen, wie sie mit dem „Sieb des Eratosthenes“ die Primzahlen bis 100 leicht finden können. Finden Sie so alle Primzahlen bis 100.

Sieve of Eratosthenes animation.gif

Quelle

Lösung

\mathbb{P}=\{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...\}

 

3. Primfaktorenzerlegung

Wir können natürliche Zahlen in Ihre „Bestandteile“ zerlegen. Das bedeutet: Wir können Sie als Produkt von Primzahlen darstellen. Dazu schreiben wir uns noch einmal die Primzahlen bis 100 auf.

\mathbb{P}=\{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...\}

Wörter 3

zerlegen, die Zerlegung, der Primfaktor, die Primfaktorenzerlegung, der Bestandteil, das Produkt, die Primzahl, darstellen, schreiben, aufschreiben, zerlegen, dividieren, klein/kleiner/am kleinsten, möglich


 
 

Beispiel

Wir zerlegen 30 in seine Primfaktoren.

30 : 2 = 15
15 : 3 = 5
5 : 5 = 1

30=2\cdot3\cdot5

Bei der Primfaktorenzerlegung dividieren wir immer durch die kleinste mögliche Primzahl.
 

Übungen

Zerlegen Sie bitte die folgenden Zahlen in ihre Primfaktoren.

20

Lösung

20=2 \cdot 2 \cdot 5

54

Lösung

54=2 \cdot 3 \cdot 3 \cdot 3

120

Lösung

120=2 \cdot 2 \cdot 2 \cdot 3 \cdot 5

600

Lösung

600=2 \cdot 2 \cdot 2 \cdot 3 \cdot 5 \cdot 5

4. Teilbarkeitsregeln

Wann ist eine Zahl teilbar? Gemeint ist „ohne Rest“. Hier zeigen wir Ihnen die wichtigsten Teilbarkeitsregeln, die Sie für die Primfaktorenzerlegung brauchen.

Wörter 4

teilen, teilbar, meinen, der Rest, zeigen, wichtig/wichtiger/am wichtigsten, die Regel, die Teilbarkeit, die Teilbarkeitsregel, zerlegen, die Zerlegung, die Primfaktorenzerlegung, der Grund, begründen


 

Die Teilbarkeitsregeln

Eine Zahl ist durch 2 teilbar, wenn sie „gerade ist“. „Gerade Zahlen“ enden auf 0, 2, 4, 6, 8. (Ungerade Zahlen enden auf 1, 3, 5, 7, 9). Beispiele: 26, 100, 2086, 395232, …

Eine Zahl ist durch 3 teilbar, wenn ihre Ziffernsumme durch 3 teilbar ist. Ziffernsumme ist die Summe ihrer Ziffern. Beispiele: 96 ist durch 3 teilbar. Die Ziffernsumme von 96 ist 9+6=15, und 15 ist durch 3 teilbar. 2118 ist durch 3 teilbar. Die Ziffernsumme von 2118 ist 12, und 12 ist durch 3 teilbar. 293817 ist durch 3 teilbar. Die Ziffernsumme von 293817 ist 30 und 30 ist durch 3 teilbar.

Eine Zahl ist durch 5 teilbar, wenn sie auf 0 oder 5 endet. Beispiele: 25, 340, 560, 1005, …

Eine Zahl ist durch 10 teilbar, wenn sie auf 0 endet. Beispiele: 10, 250, 1290, …
 

Aufgaben

Sind die folgenden Zahlen durch 2 teilbar? Begründen Sie bitte.

102

Lösung

Ja. Die Zahl endet auf 2. Das ist eine gerade Zahl.

50

Lösung

Ja. Die Zahl endet auf 0. Das ist eine gerade Zahl.

76

Lösung

Ja. Die Zahl endet auf 6. Das ist eine gerade Zahl.

85

Lösung

Nein. Die Zahl endet auf 5. Das ist eine ungerade Zahl.

103

Lösung

Nein. Die Zahl endet auf 3. Das ist eine ungerade Zahl.

Sind die folgenden Zahlen durch 3 teilbar? Begründen Sie bitte.

102

Lösung

Ja. Die Ziffernsumme ist 1+0+2=3. Und 3 ist durch 3 teilbar.

50

Lösung

Nein. Die Ziffernsumme ist 5+0=5. Und 5 ist nicht durch 3 teilbar.

76

Lösung

Nein. Die Ziffernsumme ist 7+6=13. Und 13 ist nicht durch 3 teilbar.

85

Lösung

Ja. Die Ziffernsumme ist 8+5=13. Und 3 ist nicht durch 3 teilbar.

103

Lösung

Ja. Die Ziffernsumme ist 1+0+3=4. Und 4 ist nicht durch 3 teilbar.

Sind die folgenden Zahlen durch 5 teilbar? Begründen Sie bitte.

102

Lösung

Nein. Zahl endet nicht auf 0 oder 5.

50

Lösung

Ja. Zahl endet auf 0.

76

Lösung

Nein. Zahl endet nicht auf 0 oder 5.

85

Lösung

Ja. Zahl endet auf 5.

103

Lösung

Nein. Zahl endet nicht auf 0 oder 5.

5. Warum Primzahlen

Wörter 5

leicht, hoch, finden, eigenartig, die Regelmäßigkeit, die Unregelmäßigkeit, die Spannung, sorgen, entdecken, die Entdeckung, zerlegen, die Multiplikation, die Primfaktoren, bilden, die Botschaft, der Schlüssel, verschlüsseln, wollen, verwenden, die Bösen, die Schwierigkeit, bilden, das Thema, lesen, die Wikipedia, der Artikel


 


 
Es ist nicht leicht, hohe Primzahlen zu finden. Es gibt eigenartige Regelmäßigkeiten, und eigenartige Unregelmäßigkeiten. Das sorgt für Spannung beim Entdecken. Es ist auch nicht leicht, große Zahlen in ihre Primfaktoren zu zerlegen. Es ist aber leicht, große Zahlen aus der Multiplikation von Primfaktoren zu bilden. Wenn Sie eine Botschaft verschlüsseln wollen, und Sie verwenden dazu eine große Zahl, die aus der Multiplikation von Primzahlen entstanden sind, dann werden „die Bösen“ große Schwierigkeiten haben, die Primzahlen herauszufinden, aus denen sie gebildet wurde.

Wenn Sie das Thema interessiert, lesen Sie am besten den zugehörigen Wikipedia Artikel.

6. Erweiterung

Es gibt Zikaden, die 10 Jahre als Würmer im Boden leben. Unsichtbar. Im 11. Jahr kommen alle heraus und fliegen als Insekten herum. Sie zirpen, und jeder kann sie hören. Warum aber nur jedes 11. Jahr? Haben Sie eine Idee?

Wörter 6

die Zikade, das Jahr, der Wurm, der Boden, leben, sichtbar/unsichtbar, kommen, herauskommen, fliegen, herumfliegen, das Insekt, zirpen, hören, die Idee, die Primzahl, erreichen, der Feind, sehen, nachsehen, hungern/verhungern, die Art, die Zikadenart, der Zyklus, die Entwicklung, der Entwicklungszyklus

Lösung

11 ist eine Primzahl. Sie kann durch keine andere Zahl „erreicht“ werden. Wenn ein Feind der Zikaden, jedes 2. Jahr herumfliegt, um nachzusehen, ob es Zikaden gibt, dann ist das im 2., 4., 6., 8., 10. und 12. Jahr. Nicht aber im 11. Jahr. Der Feind wird verhungern. Ein anderer Feind wird vielleicht jedes 3. Jahr herumfliegen. Das ist im 3., 6., 9., 12. Jahr, aber nicht im 11. Ein anderer Feind wird vielleicht in jedem 4. Jahr herumfliegen. Das ist im 4., 8., 12. Jahr. Aber nicht im 11. Jahr. Und so weiter. Kein Feind kann sich auf die Zikaden spezialisieren. Es gibt auch noch eine weitere Zikadenart die einen 13-jährigen Entwicklungszyklus hat. Auch das ist eine Primzahl.

 

Das war’s. Schön, dass Sie bei diesem Mathematik-Kurs dabei sind. Jeder kann Mathematik.

 

Fehler gefunden? Bitte schicken Sie ein E-Mail an fehler@phyx.at. Vielen Dank!

Kommentar absenden

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

Diese Website verwendet Akismet, um Spam zu reduzieren. Erfahre mehr darüber, wie deine Kommentardaten verarbeitet werden.